一台机器使用的时候较长,但还可以使用,它按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点零件的多少,随机器的运转的速度而变化,下表为抽样试验的结果:
| 转速χ(转/秒) |
16 |
14 |
12 |
8 |
| 每小时生产有缺点的零件数y(件) |
11 |
9 |
8 |
5 |
(1)画出散点图,并通过散点图确定变量y对χ是否线性相关;
(2)如果y对χ有线性相关关系,求回归直线方程;
(3)若实际生产中,允许每小时的产品中有缺点的零件最多为10个,那么机器的运转速度应控制在什么范围内?(精确到0.0001)
参考公式:线性回归方程的系数公式:
已知数列 满足
满足 ,且
,且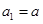 ,
,
(1)当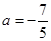 时,求出数列
时,求出数列 的所有项;
的所有项;
(2)当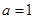 时,设
时,设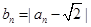 ,证明:
,证明: ;
;
(3)设(2)中的数列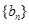 的前
的前 项和为
项和为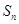 ,证明:
,证明: .
.
已知焦点在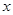 轴上的椭圆
轴上的椭圆 和双曲线
和双曲线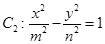 的离心率互为倒数,它们在第一象限交点的坐标为
的离心率互为倒数,它们在第一象限交点的坐标为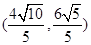 ,设直线
,设直线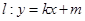 (其中
(其中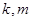 为整数).
为整数).
(1)试求椭圆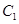 和双曲线
和双曲线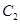 的标准方程;
的标准方程;
(2)若直线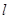 与椭圆
与椭圆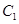 交于不同两点
交于不同两点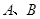 ,与双曲线
,与双曲线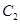 交于不同两点
交于不同两点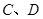 ,问是否存在直线
,问是否存在直线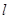 ,使得向量
,使得向量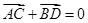 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.
已知函数 与
与 的图像都过点
的图像都过点 ,且它们在点
,且它们在点 处有公共切线.
处有公共切线.
(1)求函数 和
和 的表达式及在点
的表达式及在点 处的公切线方程;
处的公切线方程;
(2)设 ,其中
,其中 ,求
,求 的单调区间.
的单调区间.
如图,三棱柱 的侧棱与底面
的侧棱与底面 垂直,底面
垂直,底面 是等腰直角三角形,
是等腰直角三角形, ,侧棱
,侧棱 ,
, 分别是
分别是 与
与 的中点,点
的中点,点 在平面
在平面 上的射影是
上的射影是 的垂心
的垂心

(1)求证: ;
;
(2)求 与平面
与平面 所成角的大小.
所成角的大小.
选聘高校毕业生到村任职,是党中央作出的一项重大决策,这对培养社会主义新农村建设带头人、引导高校毕业生面向基层就业创业,具有重大意义。为了响应国家号召,某大学决定从符合条件的6名(其中男生4人,女生2人)报名大学生中选择3人,到某村参加村委会主任应聘考核。
(Ⅰ)设所选3人中女生人数为 ,求
,求 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)在男生甲被选中的情况下,求女生乙也被选中的概率.