如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.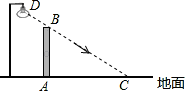
(1)求墙AB的高度(结果精确到0.1米);(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)
(2)如果要缩短影子AC的长度,同时不能改变墙的高度和位置,请你写出两种不同的方法.
如图,⊙P的圆心为P(-3,2),半径为3,直线MN过点M(5,0)且平行于y轴,点N在点M的上方,(1)在图中作出⊙P关于y轴对称的⊙P′,根据作图直接写出⊙P′与直线MN的位置关系.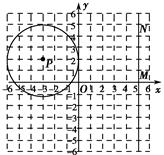
(2)若点N在(1)中的⊙P′上,求PN的长.
△ABC在平面直角坐标系中的位置如图所示.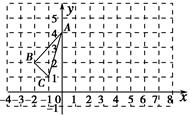
(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C1和△A2B2C2,它们是否关于某直线对称?若是,请在图上画出这条对称轴.
如图,已知正五边形ABCDE,请用无刻度的直尺,准确地画出它的一条对称轴(保留作图痕迹).
如图,在平面坐标系中,点A、点B分别在x轴、y轴的正半轴上,且OA=OB,另有两点C(a,b)和D(b,-a)(a、b均大于0);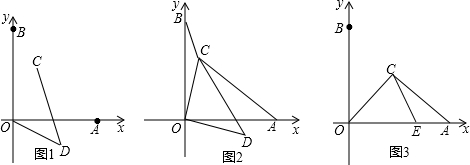
(1)连接OD、CD,求证:∠ODC=450;
(2)连接CO、CB、CA,若CB=1,C0=2,CA=3,求∠OCB的度数;
(3)若a=b,在线段OA上有一点E,且AE=3,CE=5,AC=7,求⊿OCA的面积。
已知边长为1的正方形ABCD中,点E、F分别在边BC、CD上,
(1)如图1,若AE⊥BF,求证:EA=FB;
(2)如图2,若∠EAF=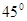 , AE的长为
, AE的长为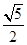 ,试求AF的长度。
,试求AF的长度。