(黄石)已知双曲线 (
( ),直线
),直线 :
: (
( k<0)过定点F且与双曲线交于A,B两点,设A(
k<0)过定点F且与双曲线交于A,B两点,设A( ,
, ),B(
),B( ,
, )(
)( ),直线
),直线 :
: .
.
(1)若 ,求△OAB的面积S;
,求△OAB的面积S;
(2)若AB= ,求k的值;
,求k的值;
(3)设N(0, ),P在双曲线上,M在直线l2上且PM∥x轴,求PM+PN最小值,并求PM+PN取得最小值时P的坐标.(参考公式:在平面直角坐标系中,若A(
),P在双曲线上,M在直线l2上且PM∥x轴,求PM+PN最小值,并求PM+PN取得最小值时P的坐标.(参考公式:在平面直角坐标系中,若A( ,
, ),B(
),B( ,
, )则A,B两点间的距离为AB=
)则A,B两点间的距离为AB= .
.
如图,已知二次函数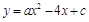 的图象与坐标轴交于点A(-1, 0)和点
的图象与坐标轴交于点A(-1, 0)和点
B(0,-5).
(1)求该二次函数的解析式;
(2)已知该函数图象的对称轴上存在一点P,使得△ABP的周长最小.请求出点P的坐标.
先阅读材料,再填空解答: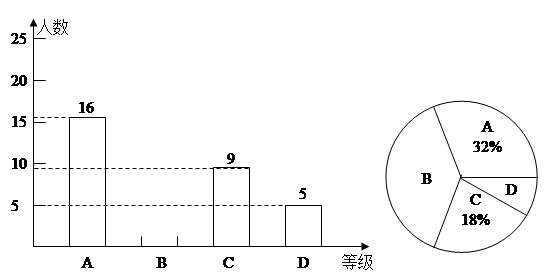 学校为了解九年级学生体育测试情况,以九年级(1)班学生的体育测试成绩为样本,按
学校为了解九年级学生体育测试情况,以九年级(1)班学生的体育测试成绩为样本,按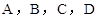 四个等级进行统计,并将统计结果绘制成如下的统计图,
四个等级进行统计,并将统计结果绘制成如下的统计图,
请你结合图中所给信息解答下列问题:(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)请把条形统计图补充完整;
(2)样本中D级的学生人数占全班学生人数的百分比是;
(3)扇形统计图中B级所在的扇形的圆心角度数是;
(4)若该校九年级有1000名学生,请你用此样本估计体育测试中A级和B级的学生人数约为人.
如图,二次函数 (
(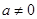 )的图象与
)的图象与 轴交于
轴交于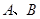 两点,与
两点,与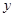 轴相交于点
轴相交于点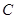 .连结
.连结 两点的坐标分别为
两点的坐标分别为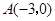 、
、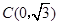 ,且当
,且当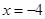 和
和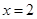 时二次函数的函数值
时二次函数的函数值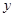 相等.
相等.
(1)求实数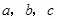 的值;
的值;
(2)若点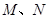 同时从
同时从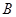 点出发,均以每秒1个单位长度的速度分别沿
点出发,均以每秒1个单位长度的速度分别沿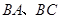 边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为
边运动,其中一个点到达终点时,另一点也随之停止运动.当运动时间为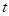 秒时,连结
秒时,连结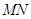 ,将
,将 沿
沿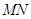 翻折,
翻折,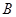 点恰好落在
点恰好落在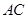 边上的
边上的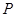 处,求
处,求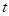 的值及点
的值及点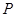 的坐标;
的坐标;
(3)在(2)的条件下,二次函数图象的对称轴上是否存在点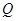 ,使得以
,使得以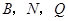 为项点的三角形与
为项点的三角形与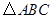 相似?如果存在,请求出点
相似?如果存在,请求出点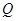 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.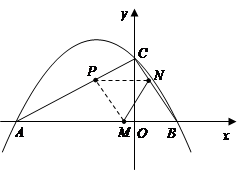
在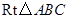 中,
中,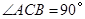 ,
,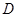 是
是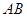 边上一点,以
边上一点,以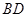 为直径的
为直径的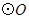 与边
与边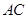 相切于点
相切于点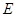 ,连结
,连结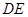 并延长,与
并延长,与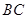 的延长线交于点
的延长线交于点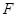 .
.
(1)求证: ;
;
(2)若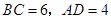 ,求
,求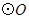 的面积.
的面积.
反比例函数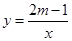 的图象如图所示,
的图象如图所示, ,
, 是该图象上的两点.
是该图象上的两点.
(1)比较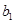 与
与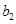 的大小;
的大小;
(2)求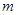 的取值范围.
的取值范围.