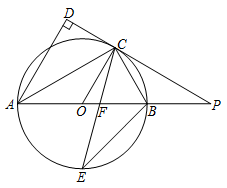
如图,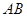 是⊙
是⊙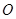 的直径,点
的直径,点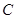 是⊙
是⊙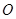 上一点,
上一点,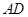 与过点
与过点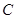 的切线垂直,垂足为点
的切线垂直,垂足为点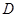 ,直线
,直线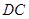 与
与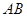 的延长线相交于点
的延长线相交于点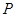 ,弦
,弦 平分∠
平分∠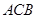 ,交
,交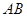 于点
于点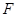 ,连接
,连接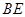 .
.
(1)求证: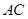 平分∠
平分∠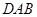 ;
;
(2)求证:PC=PF;
(3)tan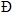 ABC=
ABC=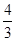 ,AB=14,求线段
,AB=14,求线段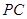 的长.
的长.
(本题6分)为了乘车方便,张强同学买了100元的乘车月票卡,如果他乘车的次数用x表示,则记录他每次乘车后的余额y(元)如下表:
(1)写出用乘车的次数x表示余额y的式子;
(2)利用上述式子,帮张强算一算乘了15次车还剩多少元?
(3)张强用100元的乘车月票卡最多乘几次车?
(本题6分)某校图书馆上周借书记录(超过100册的部分记为正,少于100册的部分记为负)如下表:
(1)上星期五借出多少册书?
(2)上星期借书最多的一天比借书最少的一天多借出图书多少册?
(3)上星期平均每天借出多少册书?
(本题8分)已知: ,
, ,当x取何值时
,当x取何值时
(1)y1与y2互为相反数?
(2)y1比y2小2?
解方程(每题4分,共8分)
(1)
(2)-
先化简,再求值(每题4分,共8分)
(1) ,其中m=-1,n=2
,其中m=-1,n=2
(2) ,其中
,其中