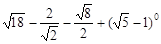如图，在平面直角坐标系中，已知点A的坐标是（4，0），并且OA=OC=4OB，动点P在过A，B，C三点的抛物线上．
（1）求抛物线的解析式；
（2）过动点P作PE垂直于y轴于点E，交直线AC于点D，过点D作x轴的垂线．垂足为F，连接EF，当线段EF的长度最短时，求出点P的坐标；
（3）是否存在点P，使得△ACP是以AC为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由．
解方程：
某开发商进行商铺促销，广告上写着如下条款：
投资者购买商铺后，必须由开发商代为租赁5年，5年期满后由开发商以比原商铺标价高20%的价格进行回购，投资者可在以下两种购铺方案中做出选择：
方案一：投资者按商铺标价一次性付清铺款，每年可以获得的租金为商铺标价的10%．
方案二：投资者按商铺标价的八五折一次性付清铺款，2年后每年可以获得的租金为商铺标价的10%，但要缴纳租金的10%作为管理费用．
（1）请问：投资者选择哪种购铺方案，5年后所获得的投资收益率更高？为什么？（注：投资收益率=
×100%）
（2）对同一标价的商铺，甲选择了购铺方案一，乙选择了购铺方案二，那么5年后两人获得的收益将相差5万元．问：甲、乙两人各投资了多少万元？
儿童节期间，文具商店搞促销活动，同时购买一个书包和一个文具盒可以打8折优惠，能比标价省13．2元．已知书包标价比文具盒标价的3倍少6元，那么书包和文具盒的标价各是多少元？
观察下列的等式
（1）
（2）
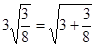（3）
… …
①发现上述3个等式的规律，猜想第5个等式并进行验证；
②写出含字母
（为任意自然数，且≥2）表示的等式，并写出证明过程。
计算：
（1）
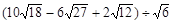
（2）