（本小题满分
分）选修
：坐标系与参数方程选讲
在直角坐标系中，以原点为极点，
轴的正半轴为极轴建立极坐标系，已知曲线
，过点
的直线
的参数方程为
（
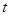为参数），与
分别交于
．
（Ⅰ）写出的平面直角坐标系方程和的普通方程；
（Ⅱ）若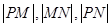
成等比数列，求
的值．
(1)如图所示，证明命题“a是平面π内的一条直线，b是π外的一条直线(b不垂直于π)，c是直线b在π上的投影，若a⊥b，则a⊥c”为真．
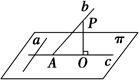
(2)写出上述命题的逆命题，并判断其真假(不需证明)．
已知p：|1－2x|≤5，q：x2－4x＋4－9m2≤0(m＞0)．若p是q的充分不必要条件，求实数m的取值范围．
已知函数f(x)＝
的定义域为集合A，函数g(x)＝lg(－x2＋2x＋m)的定义域为集合B.
(1)当m＝3时，求A∩(∁RB)；
(2)若A∩B＝{x|－1＜x＜4}，求实数m的值．
已知矩阵A＝
，B＝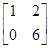
，求矩阵A－1B.
设矩阵M＝
.
(1)求矩阵M的逆矩阵M－1；
(2)求矩阵M的特征值．