某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
| 班级 |
最高分 |
平均分 |
中位数 |
众数 |
方差 |
| 九(1)班 |
100 |
m |
93 |
93 |
12 |
| 九(2)班 |
99 |
95 |
n |
93 |
8.4 |
(1)直接写出表中m、n的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.
阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得 ,(x、y为正整数)∴
,(x、y为正整数)∴ 则有0<x<6.又
则有0<x<6.又 为正整数,则
为正整数,则 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入 .
.
∴2x+3y=12的正整数解为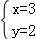
问题:
(1)请你写出方程2x+y=5的一组正整数解: ;
(2)若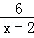 为自然数,则满足条件的x值有 个;
为自然数,则满足条件的x值有 个;
| A.2 | B.3 | C.4 | D.5 |
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
某市为了节约用水,规定:每户每月用水量不超过最低限量am3时,只付基本费8元和定额损耗费c元(c≤5);若用水量超过am3时,除了付同上的基本费和损耗费外,超过部分每1m3付b元的超额费.
根据上表的表格中的数据,求a、b、c.
2010年4月14日青海省玉树发生了7.1级大地震,驻军某部(位于距玉树县城结古镇91公里处的上拉秀镇)接到上级命令,须火速前往结古镇救援.已知该部有120名官兵,且步行的速度为每小时10公里,现仅有一辆时速为80公里的卡车,可乘坐40人,请你设计一个乘车兼步行方案,使该部120人能在最短时间内赶往重灾区结古镇救援.其中中途换车(上、下车)的时间均忽略不计,最快多少时间可以赶到?(可用分数表示)
某中学拟组织九年级师生去韶山举行毕业联欢活动.下面是年级组长李老师和小芳、小明同学有关租车问题的对话:
李老师:“平安客运公司有60座和45座两种型号的客车可供租用,60座客车每辆每天的租金比45座的贵200元.”
小芳:“我们学校八年级师生昨天在这个客运公司租了4辆60座和2辆45座的客车到韶山参观,一天的租金共计5000元.”
小明:“我们九年级师生租用5辆60座和1辆45座的客车正好坐满.”
根据以上对话,解答下列问题:
(1)平安客运公司60座和45座的客车每辆每天的租金分别是多少元?
(2)按小明提出的租车方案,九年级师生到该公司租车一天,共需租金多少元?
如图,在等腰三角形ABC中,AB=AC=10cm,∠ABC=300,以BC所在直线为x轴,以BC边上的高所在的直线为y轴建立平面直角三角形系。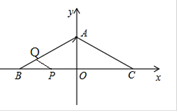
(1)求直线AC的解析式;
(2)有一动点P以1cm/s的速度从点B开始沿x轴向其正方向运动,设点P的运动为t秒(单位:s)。
①当t为何值时,ΔABP是直角三角形;
②现有另一点Q与点P同时从点B开始,以1cm/s的速度从点B开始沿折线BAC运动,当点Q到达点C时,P、Q两点同时停止运动。试写出ΔBPQ的面积S关于t的函数解析式,并写出自变量的取值范围。