（本小题满分10分）已知，如图所示，直线MN交⊙O于A，B两点，AC是直径，AD平分∠CAM交⊙O于D，过D作DE⊥MN于E，若DE=6cm，AE=3cm，求⊙O的半径．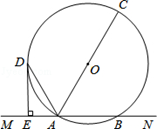
如图，点A，B在直线MN上，AB＝11厘米，⊙A，⊙B的半径均为1厘米．⊙A以每秒2厘米的速度自左向右运动，与此同时，⊙B的半径也不断增大，其半径r（厘米）与时间t（秒）之间的关系式为r＝1+t（t≥0）
试写出点A，B之间的距离d（厘米）
与时间t（秒）之间的函数表达式；问点A出发后多少秒两圆相切？
我县华联超市服装柜台在销售中发现：“宝乐”牌童装平均每天可售出20件，每件盈利40元，为了迎接“元旦”佳节，商场决定采取适当的降价措施，扩大销售量，增加盈利，尽快减少库存。经市场调查发现：如果每件童装降价4元，那么平均每天就可多售出8件，要想平均每天在销售这种童装上盈利1200元，那么每件童装应降价多少?
已知关于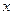
的一元二次方程
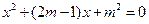有两个实数根
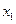和
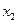．求实数
的取值范围；当
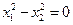时，求的值
已知
的三个顶点的坐标分别为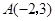
、
、
．
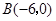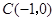请直接写出点
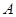关于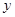
轴对称的点A
的坐标将
绕坐标原点
逆时针旋转90°．画出图形，直接写出点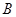
的对应点B的坐标请直接写出：以
为顶点的平行四边形的第四个顶点
的坐标
生活中的数学小明同学在某月的日历上圈出2×2个数（如图），正方形方框内的4个数的和是28，那么这4个数是
小丽同学在日历上圈出5个数，呈十字框型（如图），他们的和是65，则正中间一个数是
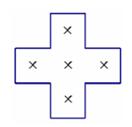
某月有5个星期日，这5个星期日的日期之和为80，则这个月中第一星期日的日期是号。
有一个数列每行8个数成一定规律排列如图：
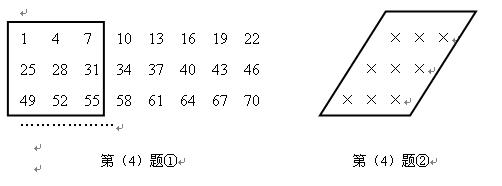
①图中方框内的9个数的和是
②小刚同学在这个数列上圈了一个斜框（如图），圈出的9个数的和为522，求正中间的一个数。