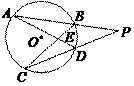如图,在平面直角坐标系中,直线 与坐标轴交于 , 两点,点 在 轴上,点 在 轴上, 点的坐标为 ,抛物线 经过点 , , .
(1)求抛物线的解析式;
(2)根据图象写出不等式 的解集;
(3)点 是抛物线上的一动点,过点 作直线 的垂线段,垂足为 点.当 时,求 点的坐标.

(10分).解方程(1)

(2)
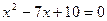
如图,直角梯形ABCD中,AD∥BC,∠A=90o,∠C=60°,AD=3cm,BC=9cm.⊙O1的圆心O1从点A开始沿折线A—D—C以1cm/s的速度向点C运动,⊙O2的圆心O2从点B开始沿BA边以 cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为ts。
cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为ts。
(1)设经过t秒,⊙O2与腰CD相切于点F,过点F画EF⊥DC,交AB于E,则EF=。
(2)过E画EG∥BC,交DC于G,画GH⊥BC,垂足为H.则∠FEG=。
(3)求此时t的值。
(4)在0<t≤3范围内,当t为何值时,⊙O1与⊙O2外切?
如图, 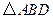 和
和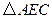 均为等边三角形,连接BE、CD.
均为等边三角形,连接BE、CD.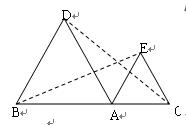
(1)请判断:线段BE与CD的大小关系是;
(2)观察图,当
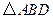 和
和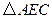 分别绕点A旋转时,BE、CD之间的大小关系是否会改变?
分别绕点A旋转时,BE、CD之间的大小关系是否会改变?
(3)观察图3和4,若四边形ABCD、DEFG都是正方形,猜想类似的结论是,在图4中证明你的猜想.

(4)这些结论可否推广到任意正多边形(不必证明),如图5,BB1与EE1的关系是;它们分别在哪两个全等三角形中;请在图6中标出较小的正六边形AB1C1D1E1F1的另五个顶点,连接图中哪两个顶点,能构造出两个全等三角形?

(本题12分).如图,在长为32 m,宽为20 m的矩形地面上修建同样宽度的道路
(图中阴影部分),余下的部分种植草坪,要使草坪的面积为540m2,求道路的宽?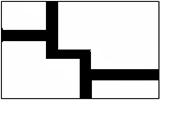
(本题10分)如图,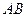 、
、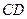 是⊙O的两条弦,延长
是⊙O的两条弦,延长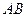 、
、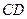 交于点
交于点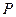 ,连结
,连结 、
、 交于
交于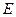 .
.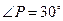 ,
,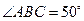 ,求
,求 的度数.
的度数.