一棉花种植区的农民研制出采摘棉花的单人便携式采棉机,采摘效率高,能耗低,绿色环保.经测试,一个人操作该采棉机的采摘效率为35公斤/时,大约是一个人手工采摘的3.5倍,购买一台采棉机需900元.雇人采摘棉花,按每采摘1公斤棉花 元的标准支付雇工工资,雇工每天工作8小时.
元的标准支付雇工工资,雇工每天工作8小时.
(1)一个雇工手工采摘棉花,一天能采摘多少公斤?
(2)一个雇工手工采摘棉花7.5天获得的全部工钱正好购买一台采棉机,求a的值;
(3)在(2)的前提下,种植棉花的专业户张家和王家均雇人采摘棉花,王家雇用的人数是张家的2倍.张家雇人手工采摘,王家所雇的人中有 的人自带采棉机采摘,
的人自带采棉机采摘, 的人手工采摘.两家采摘完毕,采摘的天数刚好一样,张家付给雇工工钱总额为14400元.王家这次采摘棉花的总重量是多少?
的人手工采摘.两家采摘完毕,采摘的天数刚好一样,张家付给雇工工钱总额为14400元.王家这次采摘棉花的总重量是多少?
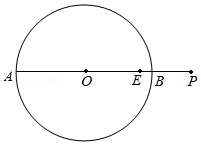
如图,点 是 的直径 延长线上的一点 ,点 是线段 的中点.
(1)尺规作图:在直径 上方的圆上作一点 ,使得 ,连接 , (保留清晰作图痕迹,不要求写作法);并证明 是 的切线;
(2)在(1)的条件下,若 , ,求 的长.
为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要 ;完成2间办公室和1间教室的药物喷洒要 .
(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?
(2)消毒药物在一间教室内空气中的浓度 (单位: 与时间 (单位: 的函数关系如图所示:校医进行药物喷洒时 与 的函数关系式为 ,药物喷洒完成后 与 成反比例函数关系,两个函数图象的交点为 .当教室空气中的药物浓度不高于 时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算说明.

有一个可自由转动的转盘,被分成了三个大小相同的扇形,分别标有数字2,4,6;另有一个不透明的瓶子,装有分别标有数字1,3,5的三个完全相同的小球.小杰先转动一次转盘,停止后记下指针指向的数字(若指针指在分界线上则重转),小玉再从瓶子中随机取出一个小球,记下小球上的数字.
(1)请用列表或画树状图的方法(选其中一种)表示出所有可能出现的结果;
(2)若得到的两数字之和是3的倍数,则小杰贏;若得到的两数字之和是7的倍数,则小玉赢,此游戏公平吗?为什么?

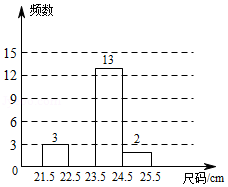
某鞋店在一周内销售某款女鞋,尺码(单位: 数据收集如下:
|
24 |
23.5 |
21.5 |
23.5 |
24.5 |
23 |
22 |
23.5 |
23.5 |
23 |
22.5 |
23.5 |
23.5 |
22.5 |
24 |
|
24 |
22.5 |
25 |
23 |
23 |
23.5 |
23 |
22.5 |
23 |
23.5 |
23.5 |
23 |
24 |
22 |
22.5 |
绘制如图不完整的频数分布表及频数分布直方图:
|
尺码 |
划记 |
频数 |
|
|
|
3 |
|
|
|
|
|
|
|
13 |
|
|
|
2 |
(1)请补全频数分布表和频数分布直方图;
(2)若店主要进货,她最应该关注的是尺码的众数,上面数据的众数为 ;
(3)若店主下周对该款女鞋进货120双,尺码在 范围的鞋应购进约多少双?
如图, 是 的平分线,点 是线段 上的一点, , .求证: .
