如图,△ABC为等边三角形,以边BC为直径的半圆与边AB,AC分别交于D,F两点,过点D作DE⊥AC,垂足为点E.
(1)判断DF与⊙O的位置关系,并证明你的结论;
(2)过点F作FH⊥BC,垂足为点H,若AB=4,求FH的长(结果保留根号).
水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种80千克的钱,现在可买88千克。
(1)现在实际这种每千克多少元?
(2)准备这种,若这种的量y(千克)与单价x(元/千克)满足如图所示的一次函数关系。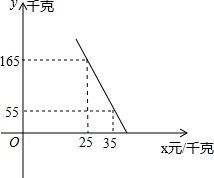
①求y与x之间的函数关系式;
②请你帮拿个主意,将这种的单价定为多少时,能获得最大利润?最大利润是多少?(利润=收入-进货金额)
实践操作:如图,△ABC是直角三角形,∠ACB=900,利用直尺和圆规按下列要求作图,并在图中表明相应的字母。(保留痕迹,不写作法)
(1)作BAC的平分线,交BC于点O;
(2)以O为圆心,OC为半径作圆。
综合运用:在你所作的图中,
(1)AB与⊙O的位置关系是;(直接写出答案)
(2)若AC=5,BC=12,求⊙O的半径。
如图,在平行四边形ABCD中,E为BC边上一点,连结AE、BD且AE=AB。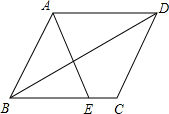
(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形。
一只不透明的袋子中,装有分别标有数字1、2、3的三个球,这些除所外都相同,搅匀后从摸出个,记录下后放回袋并搅匀,再从任意摸出个,记录下,请用列表或画树状图方法,求出两次摸出上之和为偶数概率.
市交警支队对某校学生进行交通安全知识宣传,事先以无记名的方式随机调查了该部分闯红灯的情况,并绘制成如图所示的统计图.请根据图中的信息回答下列问题: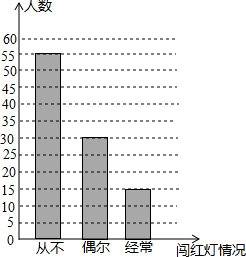
(1)本次共调查了多少名?
(2)如果该共有1500名,请你估计该经常闯红灯的大约有多少人;
(3)针图中反映的信息谈谈你的认识.(不超过30个字)。