阅读资料：
如图1，在平面之间坐标系xOy中，A，B两点的坐标分别为A（x1，y1），B（x2，y2），由勾股定理得AB2=|x2﹣x1|2+|y2﹣y1|2，所以A，B两点间的距离为AB=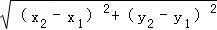
．
我们知道，圆可以看成到圆心距离等于半径的点的集合，如图2，在平面直角坐标系xoy中，A（x，y）为圆上任意一点，则A到原点的距离的平方为OA2=|x﹣0|2+|y﹣0|2，当⊙O的半径为r时，⊙O的方程可写为：x2+y2=r2．
问题拓展：如果圆心坐标为P（a，b），半径为r，那么⊙P的方程可以写为 ．
综合应用：
如图3，⊙P与x轴相切于原点O，P点坐标为（0，6），A是⊙P上一点，连接OA，使tan∠POA=
，作PD⊥OA，垂足为D，延长PD交x轴于点B，连接AB．
①证明AB是⊙P的切点；
②是否存在到四点O，P，A，B距离都相等的点Q？若存在，求Q点坐标，并写出以Q为圆心，以OQ为半径的⊙O的方程；若不存在，说明理由．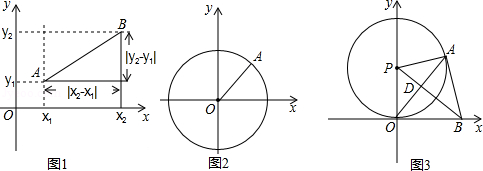
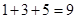
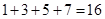
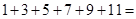
（1）第5个式子等号右边应填的数是；
（2）根据规律填空1＋3＋5＋7＋…＋(2n-1)＝；
（3）计算：1＋3＋5＋7＋…＋2013 ＝.
计算（1）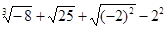
（2）
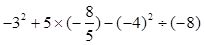
（3）
（4）
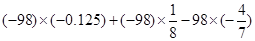
把下列各数填在相应的表示集合的大括号内：
－2 ，π，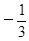
，
，
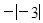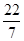，－0.3，1.7，
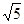，0 ， 1.1010010001……（每两个1之间依次多一个0）整数{ }
负分数{ }
无理数{ }
阅读理解题（本题共14分）
如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动。它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走为正，向下向左走为负。如果从A到B记为：A→B（＋1，＋4），从B到A记为：A→B（－1，－4），其中第一个数表示左右方向，第二个数表示上下方向，那么图中
（1）A→C（，），B→C（，）,C→（＋2，）；
（2）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程；
（3）若这只甲虫从A处去甲虫P处的行走路线依次为（＋2，＋2），（＋2，－1），（－2，＋3），（－1，－2），请在图中标出P的位置。
（4）请你为这只甲壳虫设计一种从A处去往E处的路线。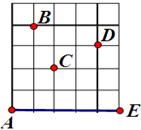
观察下列各式。
，
，
，
…… …
(1)猜想填空：
( )2
( )2
（2）求
的值