（本小题满分9分）为提高饮水质量，越来越多的居民开始选购家用净水器，一商场抓住商机，从厂家购进A、B两种型号家用净水器共160台，A型号家用净水器进价是150元/台，B型号家用净水器进价是350元/台，购进两种型号的家用净水器共用去36000元，
（1）求A、B两种型号家用净水器各购进多少台？
（2）为使每台B型号家用净水器的毛利润是A型号的2倍，且保证售完这160台家用净水器的毛利润不低于11000元，求每台A型号家用净水器的售价至少是多少元．（注：毛利润=售价-进价）
已知，如图AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE=DF．
如图， AC与BD交于点E，且AC=DB，AB=DC．求证：∠A=∠D；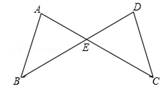
如图，已知直线l的函数表达式为
，且l与x轴、y轴分别交于A、B两点，动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动，同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动，设点Q、P移动时间为t秒。
（1）求点A、B的坐标。
（2）当t为何值时，以点A、P、Q为顶点的三角形与△AOB相似？
如图所示，梯形ABCD中，AD∥BC，点E是边AD的中点，连接BE交AC于点F，BE的延长线交CD的延长线于点G。
（1）求证：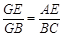
；
（2）若GE=2，BF=3，求线段EF的长。
如图，在△ABC中，∠BAC=90°，AB=AC，BE平分∠ABC，CE⊥BE，垂足为E．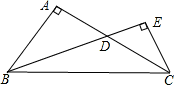
（1）求证：BD•BE=AB•BC；
（2）延长CE、BA交于F，求证：CF=BD．