某校为调研学生的身高与运动量之间的关系,从高二男生中随机抽取100名学生的身高数据,得到如下频率分布表:
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
[160,165) |
10 |
0.100 |
| 第2组 |
[165,170) |
① |
0.150 |
| 第3组 |
[170,175) |
30 |
② |
| 第4组 |
[175,180) |
25 |
0.250 |
| 第5组 |
[180,185) |
20 |
0.200 |
| 合计 |
100 |
1.00 |
(1)求频率分布表中①、②位置相应的数据;
(2)为了对比研究学生运动量与身高的关系,学校计划采用分层抽样的方法从第2、5组中随机抽取7名学生进行跟踪调研,求第2、5组每组抽取的学生数?
(3)在(2)的前提下,学校决定从这7名学生中随机抽取2名学生接受调研访谈,求至少有1名学生来自第5组的概率?
设函数 ,其中
,其中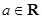 .
.
(1)若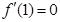 ,求a的值;
,求a的值;
(2)当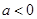 时,讨论函数
时,讨论函数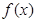 在其定义域上的单调性.
在其定义域上的单调性.
某市旅游部门开发一种旅游纪念品,每件产品的成本是 元,销售价是
元,销售价是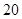 元,月平均销售
元,月平均销售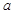 件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为
 ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为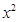 .记改进工艺后,旅游部门销售该纪念品的月平均利润是
.记改进工艺后,旅游部门销售该纪念品的月平均利润是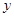 (元).
(元).
(1)写出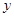 与
与 的函数关系式;
的函数关系式;
(2)改进工艺后,确定该纪念品的售价,使旅游部门销售该纪念品的月平均利润最大.
在数列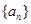 中,
中, ,
, ,
, 。
。
(Ⅰ)计算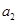 ,
,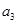 ,
, 的值;
的值;
(Ⅱ)猜想数列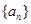 的通项公式,并用数学归纳法加以证明
的通项公式,并用数学归纳法加以证明
设函数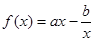 ,曲线
,曲线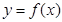 在点
在点 处的切线方程为7x-4y-12=0,求
处的切线方程为7x-4y-12=0,求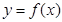 的解析式和
的解析式和 .
.
如图:是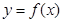 =
=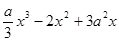 的导函数
的导函数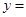
 的简图,它与
的简图,它与 轴的交点是(1,0)和(3,0)
轴的交点是(1,0)和(3,0)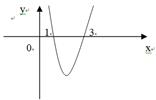
(1)求 的极小值点和单调区间;
的极小值点和单调区间;
(2)求实数 的值.
的值.