如图,某污水处理厂要在一个矩形 的池底水平铺设污水净化管道(直角
的池底水平铺设污水净化管道(直角 ,
, 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口 是
是 的中点,
的中点, 分别落在
分别落在
 上,且
上,且 ,设
,设 .
.
(1)试将污水管道的长度 表示成
表示成 的函数,并写出定义域;
的函数,并写出定义域;
(2)当管道长度 为何值时,污水净化效果最好,并求此时管道的长度.
为何值时,污水净化效果最好,并求此时管道的长度.
在区间(0,1)中随机地取两个数X,Y,求这两个数X,Y中较小的数小于 的概率。
的概率。
甲盒中有红,黑,白三种颜色的球各2个,乙盒子中有黄,黑,白,
三种颜色的球各2个,从两个盒子中各取1个球,
(1)求取出的两个球是不同颜色的概率.
(2)请设计一种随机模拟的方法,来近似计算(1)中取出两个球是不同
颜色的概率(写出模拟的步骤)
(8分)有一个容量为100的样本,数据的分组及各组的频数如下:
(1)列出样本的频率分布表;
(2)画出频率分布直方图和频率折线图。
设计一个计算1+ +
+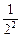 +
+ +…+
+…+ .的算法,并编写程序.
.的算法,并编写程序.
某市电信部门规定:拔打市内电话时,如果通话时间不超过3分钟,则收取通话费0.2元,如果通话时间超过3分钟,则超过部分以每分钟0.1元收取通话费(通话时间以分钟计,不足1分钟时按1分 钟计),试设计一个计算通话费的算法,并画出程序框
钟计),试设计一个计算通话费的算法,并画出程序框 图。
图。