如图，对称轴为直线x=−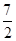
的抛物线经过点A（-6，0）和点B（0，4）．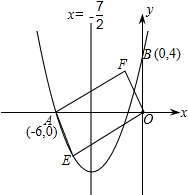
（1）求抛物线的解析式和顶点坐标；
（2）设点E（x，y）是抛物线上的一个动点，且位于第三象限，四边形OEAF是以OA为对角线的平行四边形，求▱OEAF的面积S与x的函数关系式，并写出自变量x的取值范围；
①当▱OEAF的面积为24时，请判断▱OEAF是否为菱形？
②是否存在点E，使▱OEAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由．
解方程：
.
（本题每小题6分，满分12分.）
（1）计算：|－
|÷|
－
| －
×
.
（2）先化简，再求值：
，其中
，y=-2.
用棋子摆出下列一组三角形,三角形每边有
枚棋子,每个三角形的棋子总数是
.按此规律推断,当三角形边上有枚棋子时,该三角形的棋子总数等于 :
A． |
B． |
C． |
D． |
（1）.如图①，已知AB∥CD，求证：∠A+∠C=∠E
（2）直接写出当点E的位置分别如图②、图③、图④的情形时∠A、∠C、∠E之间的关系.
②中∠C、∠A、∠AEC之间的关系为；
③中∠C、∠A、∠AEC之间的关系为；
④中∠C、∠A、∠AEC之间的关系为；
（3）在（2）中的3中情形中任选一种进行证明.
如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的中点，过点A作AD⊥AB交BE的延长线于点D，CG平分∠ACB交BD于点G，F为AB边上一点，连接CF，且∠ACF＝∠CBG .
求证：（1）BG＝CF；
（2）DG=CF