如图所示，半径R=0.6m的光滑圆弧轨道BCD与足够长的粗糙轨道DE在D处平滑连接，O为圆弧轨道BCD的圆心，C点为圆弧轨道的最低点，半径OB、OD与OC的夹角分别为53°和37°。将一个质量m=0.5kg的物体(视为质点)从B点左侧高为h=0.8m处的A点水平抛出，恰从B点沿切线方向进入圆弧轨道。已知物体与轨道DE间的动摩擦因数
=0.8，重力加速度g取10m/s2，sin37°="0." 6，cos37°=0.8。求：
（1）物体水平抛出时的初速度大小v0；
（2）物体在轨道DE上运动的路程s。
如图所示，两平行金属板水平放置,板间存在竖直向下的勻强电场。一带电粒子以初速度V0沿上板边缘垂直于电场线射入匀强电场，它刚好贴着下板边缘飞出。已知匀强电场两极板长L，间距为d，（粒子的重力忽略不计）求：
⑴如果带电粒子的初速度变为2V0，则离开电场时，沿场强方向的侧向位移y为多少？
⑵如果带电粒子的初速度变为2V0，粒子离开电场后继续运动，当它的竖直位移仍为d时，它的水平位移x为多少？
(3)如果带电粒子的初速度变为2V0，粒子离开电场时动能与带电粒子以初速度V0射入匀强电场后离开电场时动能之比？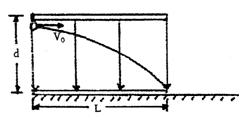
如图所示的电路，电源电动势E=9v，电阻R1=2.5Ω,R2=3Ω,当变阻器R调到3Ω时，电流表示数为2A。
试求；(1)电源的内阻。
(2)调节变阻器，使电流表示数为2.5A时接入变阻器R的阻值。
(3)调节变阻器，使电流表示数为2.5A时变阻器R消耗的功率。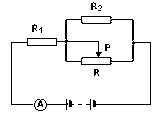
光滑水平面上相距为L的A,B两个带正电小球电量分别为4Q和Q。要在它们之间引入第三个带电小球C，使三个小球都只在相互库仑力作用下而处于平衡，求：
（1）小球C带何种电？
（2）电量q为多大？
（3）C与A之间的距离x等于多大?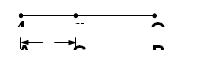
如图所示，回旋加速器的半径为R，匀强磁场的磁感应强度为B，高频电场的电压为U，S0为粒子源，S’为引出口．若被加速的粒子质量为m,电荷量为q，设带电粒子质量不变，且不考虑粒子从粒子源射出时的能量．问：
（1）外加电
场的变化周期为多少？
（2）粒子从加速器中射出时的能量为多少？
（3）粒子以加速器中被加速的时间共为多少？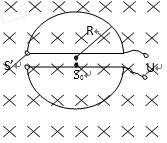
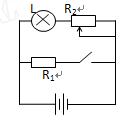
图中电阻R1＝6Ω,滑动变阻器R2的最大阻值为10Ω,开始调至2Ω,电源电阻r=1Ω.当S闭合时，电源的总功率为16W，电源输出功率为12W．这时灯L正常发光．试求：
（1）灯L的额定功率为多少？
（2）S断开时，灯L的实际功率为多少？
（3）要使L正常发光滑动变阻器的阻值应调至多大？