【2015高考上海,文21】(本小题14分)本题共2小题,第1小题6分,第2小题8分.
如图,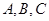 三地有直道相通,
三地有直道相通,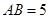 千米,
千米,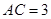 千米,
千米,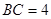 千米.现甲、乙两警员同时从
千米.现甲、乙两警员同时从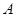 地出发匀速前往
地出发匀速前往 地,经过
地,经过 小时,他们之间的距离为
小时,他们之间的距离为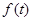 (单位:千米).甲的路线是
(单位:千米).甲的路线是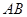 ,速度为5千米/小时,乙的路线是
,速度为5千米/小时,乙的路线是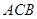 ,速度为8千米/小时.乙到达
,速度为8千米/小时.乙到达 地后原地等待.设
地后原地等待.设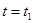 时乙到达
时乙到达 地.
地.
(1)求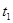 与
与 的值;
的值;
(2)已知警员的对讲机的有效通话距离是3千米.当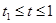 时,求
时,求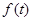 的表达式,并判断
的表达式,并判断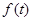 在
在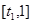 上得最大值是否超过3?说明理由.
上得最大值是否超过3?说明理由.
(本题满分14分)
如图,两个工厂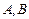 相距
相距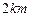 ,点
,点 为
为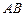 的中点,现要在以
的中点,现要在以 为圆心,
为圆心,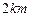 为半
为半 径的圆弧
径的圆弧 上的某一点
上的某一点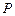 处建一幢办公楼,其中
处建一幢办公楼,其中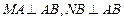 .据测算此办公楼受工厂
.据测算此办公楼受工厂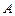 的“噪音影响度”与距离
的“噪音影响度”与距离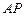 的平方成反比,比例系数是1,办公楼受工厂
的平方成反比,比例系数是1,办公楼受工厂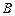 的“噪音影响度” 与距离
的“噪音影响度” 与距离
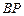 的平方也成反比,比例系数是4,办公楼受
的平方也成反比,比例系数是4,办公楼受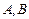 两厂的“总噪音影响度”
两厂的“总噪音影响度”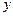 是受
是受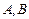 两厂“噪音影响度”的和,设
两厂“噪音影响度”的和,设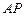 为
为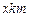 .
.
(Ⅰ)求“总噪音影响度” 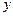 关于
关于 的函数关系,
的函数关系,
并求出该函数的定义域;
(Ⅱ)当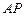 为多少时,“总噪音影响度”最小?
为多少时,“总噪音影响度”最小?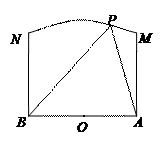
(本题满分14分)
已知椭圆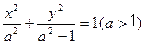 的左右焦点为
的左右焦点为 ,抛物线C:
,抛物线C: 以F2为焦点且与椭圆相交于点M,直线F1M与抛物线C相切。
以F2为焦点且与椭圆相交于点M,直线F1M与抛物线C相切。
(Ⅰ)求抛物线C的方程和点M的坐标;
(Ⅱ)过F2作抛物线C的两条互相垂直的弦AB、DE,设弦AB、DE的中点分别为F、N,求证直线FN恒过定点;
(本小题满分14分)
某大学开设甲、乙、丙三门选修课,学生是否选修哪门课互不影响. 已知学生小张只选甲的概率为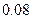 ,只选修甲和乙的概率是
,只选修甲和乙的概率是 ,至少选修一门的概率是
,至少选修一门的概率是 ,用
,用 表示小张选修的课程门数和没有选修的课程门数的乘积.
表示小张选修的课程门数和没有选修的课程门数的乘积.
(Ⅰ)求学生小张选修甲的概率;
(Ⅱ)记“函数
 为
为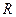 上的偶函数”为事件
上的偶函数”为事件 ,求事件
,求事件 的概率;
的概率;
(Ⅲ)求 的分布列和数学期望。
的分布列和数学期望。
(本小题满分12分)
如图,在三棱锥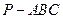 中,
中,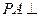 底面ABC,
底面ABC, ,
,
AP="AC," 点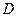 ,
, 分别在棱
分别在棱 上,且BC//平面ADE
上,且BC//平面ADE
(Ⅰ)求 证:DE⊥平面
证:DE⊥平面
 ;
;
(Ⅱ)当二面角 为直二面角时,求多面体ABCED与PAED的体积比。
为直二面角时,求多面体ABCED与PAED的体积比。
(本小题满分12分)
已知函数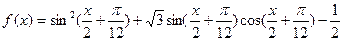 。
。
(Ⅰ)求 的值域;
的值域;
(Ⅱ)若 (x>0)的图象与直线
(x>0)的图象与直线 交点的横坐标由小到大依次是
交点的横坐标由小到大依次是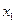 ,
,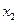 ,…,
,…,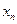 ,求数列
,求数列 的前
的前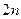 项的和。
项的和。