【2015高考湖北,理17】某同学用“五点法”画函数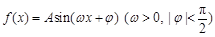 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
 |
0 |
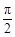 |
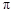 |
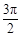 |
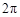 |
 |
|
 |
|
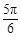 |
|
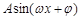 |
0 |
5 |
|
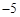 |
0 |
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数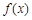 的解析式;
的解析式;
(Ⅱ)将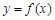 图象上所有点向左平行移动
图象上所有点向左平行移动
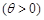 个单位长度,得到
个单位长度,得到 的图象.若
的图象.若 图象的一个对称中心为
图象的一个对称中心为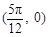 ,求
,求 的最小值.
的最小值.
已知函数
(Ⅰ)求 的单调减区间;
的单调减区间;
(Ⅱ)若 在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
在区间[-2,2].上的最大值为20,求它在该区间上的最小值.
某防疫站对屠宰场及肉食零售点的猪肉检查沙门氏菌带菌情况,结果如下表,试检查屠宰场与零售点猪肉带菌有无差异
| 带菌头数 |
不带菌头数 |
合计 |
|
| 屠宰场 |
8 |
32 |
40 |
| 零售店 |
14 |
18 |
32 |
| 合计 |
22 |
50 |
72 |
( )
)
商场销售某种商品的经验表明,该商品每日的销售量
(单位:千克)与销售价格
(单位:元/千克)满足关系式
,其中
,
为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.
(1) 求
的值;
(2) 若商品的成品为3元/千克, 试确定销售价格
的值,使商场每日销售该商品所获得的利润最大
已知一条曲线 在 轴右边, 上每一点到点 的距离减去它到 轴距离的差都是 .
(1)求曲线
的方程.
(2)是否存在正数
,对于过点
且与曲线
有两个交点
的任一直线,都有
?若存在,求出m的取值范围,若不存在,请说明理由.
已知函数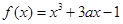 ,
, ,其中
,其中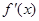 是
是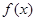 的导函数.
的导函数.
(1)对满足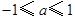 的一切
的一切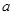 的值,都有
的值,都有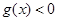 ,求实数
,求实数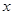 的取值范围;
的取值范围;
(2)设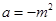 ,当实数
,当实数 在什么范围内变化时,函数
在什么范围内变化时,函数 的图象与直线
的图象与直线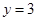 只有一个公共点.
只有一个公共点.