【2015高考山东,理19】若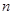 是一个三位正整数,且
是一个三位正整数,且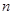 的个位数字大于十位数字,十位数字大于百位数字,则称
的个位数字大于十位数字,十位数字大于百位数字,则称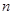 为“三位递增数”(如137,359,567等).在某次数学趣味活动中,每位参加者需从所有的“三位递增数”中随机抽取1个数,且只能抽取一次.得分规则如下:若抽取的“三位递增数”的三个数字之积不能被5整除,参加者得0分;若能被5整除,但不能被10整除,得
为“三位递增数”(如137,359,567等).在某次数学趣味活动中,每位参加者需从所有的“三位递增数”中随机抽取1个数,且只能抽取一次.得分规则如下:若抽取的“三位递增数”的三个数字之积不能被5整除,参加者得0分;若能被5整除,但不能被10整除,得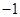 分;若能被10整除,得1分.
分;若能被10整除,得1分.
(Ⅰ)写出所有个位数字是5的“三位递增数” ;
(Ⅱ)若甲参加活动,求甲得分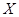 的分布列和数学期望
的分布列和数学期望 .
.
如图, 是圆
是圆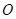 的直径,点
的直径,点 是圆
是圆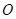 上异于
上异于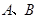 的点,直线
的点,直线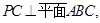
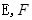 分别为
分别为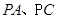 的中点。
的中点。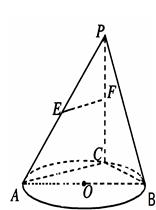
(1)记平面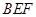 与平面
与平面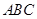 的交线为
的交线为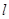 ,试判断
,试判断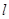 与平面
与平面 的位置关系,并加以说明;
的位置关系,并加以说明;
(2)设(1)中的直线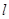 与圆
与圆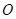 的另一个交点为
的另一个交点为 ,且点
,且点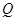 满足
满足 ,记直线
,记直线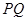
平面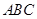 所成的角为
所成的角为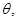 异面直线
异面直线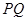 与
与 所成的锐角为
所成的锐角为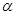 ,二面角
,二面角 的大小为
的大小为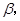
①求证: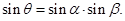
②当点 为弧
为弧 的中点时,
的中点时,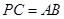 ,求直线
,求直线 与平面
与平面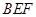 所成的角的正弦值。
所成的角的正弦值。
如图,在等腰直角三角形 中,
中, 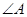 =900 ,
=900 , ="6,"
="6,"  分别是
分别是 ,
,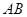 上的点,
上的点,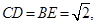
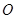 为
为 的中点.将
的中点.将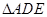 沿
沿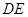 折起,得到如图所示的四棱椎
折起,得到如图所示的四棱椎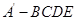 ,其中
,其中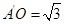


(1)证明: ;
;
(2)求二面角 的平面角的余弦值.
的平面角的余弦值.
如图所示,在三棱柱 中,
中,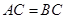 ,
,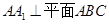 ,点
,点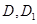 分别是
分别是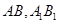 的中点.
的中点.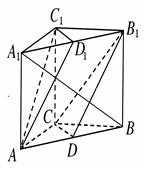
(1)求证:平面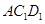 ∥平面
∥平面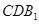 ;
;
(2)求证:平面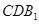 ⊥平面
⊥平面 ;
;
(3)若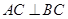 ,
, ,求异面直线
,求异面直线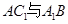 所成的角。
所成的角。
已知圆台的上、下底面半径分别是2、6,且侧面面积等于两底面面积之和。
(1)求该圆台的母线长;(2)求该圆台的体积。
(1)求经过点A(3,2),B(-2,0)的直线方程。
(2)求过点P(-1,3),并且在两轴上的截距相等的直线方程;