请在下面直线上任意取一点O，并以O点为圆心画一个直径为4厘米的圆．在圆上挖取一个最大的正方形．（剩下的用阴影表示）计算这个阴影部分的面积．
．
如图，在△ABC中，AD、CE是两条高，连结DE，如果BE=2，EA=3，CE=4，在不添加任何辅助线和字母的条件下，请写出三个正确结论（要求：分别为边的关系，角的关系，三角形相似的关系），并对其中三角形相似的结论给予证明.
边的关系;
角的关系;
三角形相似的关系.
证明:
已知当压力不变时，木板对地面的压强p(Pa)是木板面积S（m2）的反比例函数，其图象如图所示.
（1）请直接写出p与S之间的关系式和自变量S的取值范围；
（2）当木板面积为2 m2时，压强是多少？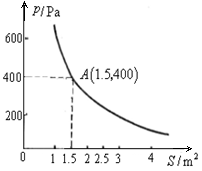
计算：
如图，在平面直角坐标系中，四边形OABC是矩形，OA = 6，AB = 4，直线y =" -" x +3与坐标轴交于D、E。设M是AB的中点，P是线段DE上的动点.
（1）求M、D两点的坐标；
（2）当P在什么位置时，PA = PB？求出此时P点的坐标；
（3）过P作PH⊥BC，垂足为H，当以PM为直径的⊙F与BC相切于点N时，求梯形PMBH的面积.
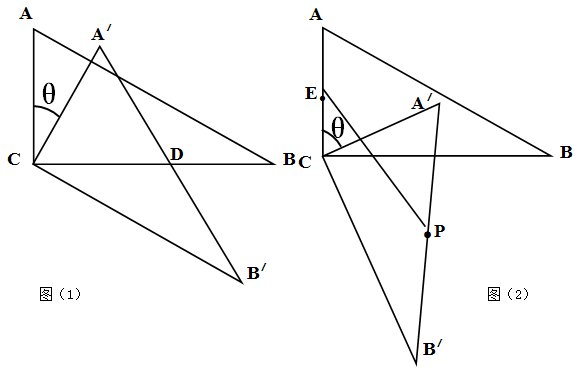
在△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕顶点C顺时针旋转，旋转角为
（0°＜＜180°），得到△A′B′C．
（1）如图（1），当AB∥CB′时，设A′B′与CB相交于点D．证明：△A′CD是等边三角形；
（2）如图（2），设AC中点为E，A′B′中点为P，AC=
，连接EP， 当=°时，EP长度最大，最大值为．