（本题10分）古希腊著名的毕达哥拉斯学派把1、3、6、10 …，这样的数称为“三角形数”，而把1、4、9、16…，这样的数称为“正方形数”．
（1）第5个三角形数是 ，第n个“三角形数”是 ，第5个“正方形数”是 ，第n个正方形数是 ；
（2）经探究我们发现：任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．
例如：①4=1+3，②9=3+6，③16=6+10，④ ，⑤ ，…．
请写出上面第4个和第5个等式；
（3）在（2）中，请探究第n个等式，并证明你的结论．
直线y=kx+b交坐标轴于A（－2，0），B（0，3）两点，
|
求不等式kx+b＞0的解集．
如图1，在平面直角坐标系中，第一象限内长方形ABCD ， AB∥y轴，点A（1，1），点C（a， b）， 满足
．
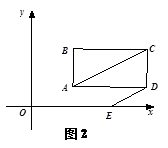
（1）求长方形ABCD的面积．
（2）如图2，长方形ABCD以每秒1个单位长度的速度向右平移，同时点E从原点O出发沿x轴以每秒2 个单位长度的速度向右运动，设运动时间为t秒．
①当t=4时，直接写出三角形OAC的面积为_______．
② 若AC∥ED，求t 的值;
（3）在平面直角坐标系中，对于点
，我们把点
叫做点
的伴随点，已知点
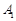的伴随点为
，点的伴随点为
，点的伴随点为
，…，这样依次得到点，，，…，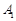
．
①若点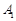的坐标为（3，1），则点的坐标为，点
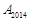的坐标为；
②若点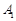的坐标为（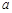
，
），对于任意的正整数
，点均在
轴上方，则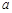，应满足的条件为．
直线EF、GH之间有一个直角三角形ABC，其中∠BAC = 90°，∠ABC =
．
（1）如图1，点A在直线EF上，B、C在直线GH上，若∠=60°，∠FAC =30°．求证：EF∥GH;
（2）将三角形ABC如图2放置，直线EF∥GH，点C 、B分别在直线EF、GH上，且BC平分∠ABH，直线CD平分∠FCA交直线GH于D．在取不同数值时，∠BCD的大小是否发生变化？若不变求其值，若变化指出其变化范围．
小武新家装修，在装修客厅时，购进彩色地砖和单色地砖共100块，共花费5600元．已知彩色地砖的单价是80元/块，单色地砖的单价是40元/块．
（1）两种型号的地砖各采购了多少块？
（2）如果厨房也要铺设这两种型号的地砖共60块，且采购地砖的费用不超过3200元，那么彩色地砖最多能采购多少块？
如图所示的平面直角坐标系中， 将△ABC平移后得到△DEF．已知B点平移的对应点E点（0，－3）（A点与D点对应，C点与F点对应）．
（1）△ABC的面积为 ;
（2）画出平移后的△DEF，并写出点D的坐标为，点F的坐标为;
（3）若线段DF交y轴于P， 则点P的坐标为．