【2015高考陕西,理18】(本小题满分12分)如图 ,在直角梯形
,在直角梯形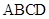 中,
中,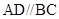 ,
,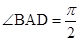 ,
,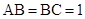 ,
, ,
,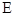 是
是 的中点,
的中点,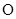 是
是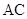 与
与 的交点.将
的交点.将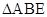 沿
沿 折起到
折起到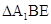 的位置,如图
的位置,如图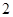 .
.
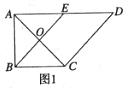
(Ⅰ)证明: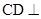 平面
平面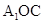 ;
;
(Ⅱ)若平面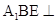 平面
平面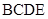 ,求平面
,求平面 与平面
与平面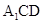 夹角的余弦值.
夹角的余弦值.
已知等比数列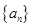 中
中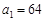 ,公比
,公比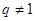 ,且
,且 ,
,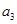 ,
,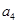 分别为某等差数列的第5项, 第3项,第2项.
分别为某等差数列的第5项, 第3项,第2项.
(1)求数列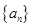 的通项公式;(2)设
的通项公式;(2)设 ,求数列
,求数列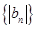 的前
的前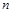 项和
项和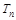 .
.
如图所示,在棱长为2的正方体 中,点
中,点 分别在棱
分别在棱 上,满足
上,满足 ,且
,且 .
.
(1)试确定 、
、 两点的位置.
两点的位置.
(2)求二面角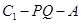 大小的余弦值.
大小的余弦值.
(文)如图,在四棱锥 中,四边形
中,四边形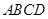 是菱形,
是菱形,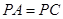 ,
,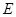 为
为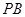 的中点.
的中点.
(1)求证: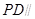 面
面 ;
;
(2)求证:平面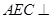 平面
平面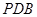 .
.
(1)已知矩阵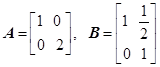 ,若矩阵
,若矩阵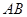 对应的变换把直线
对应的变换把直线 :
: 变为直线
变为直线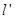 ,求直线
,求直线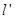 的方程.
的方程.
(2)在极坐标系中,圆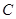 的方程为
的方程为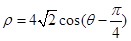 ,以极点为坐标原点,极轴为
,以极点为坐标原点,极轴为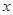 轴 的正半轴建立平面直角坐标系,直线
轴 的正半轴建立平面直角坐标系,直线 的参数方程为
的参数方程为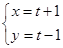 (
(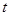 为参数),求直线
为参数),求直线 被 圆
被 圆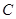 截得的弦
截得的弦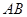 的长度.
的长度.
(文)在平面直角坐标系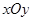 中,设锐角
中,设锐角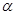 的始边与
的始边与 轴的非负半轴重合,终边与单位 圆交于点
轴的非负半轴重合,终边与单位 圆交于点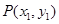 ,将射线
,将射线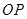 绕坐标原点
绕坐标原点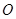 按逆时针方向旋转
按逆时针方向旋转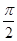 后与单位圆交于点
后与单位圆交于点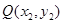 .记
.记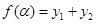 .(1)求函数
.(1)求函数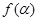 的值域;(2)设
的值域;(2)设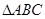 的角
的角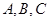 所对的边分别为
所对的边分别为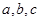 ,若
,若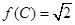 ,且
,且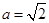 ,
,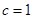 ,求
,求 .
.