(文)如图,在四棱锥 中,四边形
中,四边形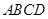 是菱形,
是菱形,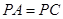 ,
,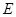 为
为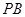 的中点.
的中点.
(1)求证: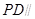 面
面 ;
;
(2)求证:平面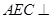 平面
平面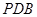 .
.
(本小题满分14分)已知函数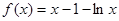
(1)求曲线 在点
在点 处的切线方程;
处的切线方程;
(2)求函数 的极值;
的极值;
(3)对 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知函数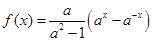 ,其中
,其中
(1)写出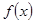 的奇偶性与单调性(不要求证明);
的奇偶性与单调性(不要求证明);
(2)若函数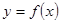 的定义域为
的定义域为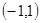 ,求满足不等式
,求满足不等式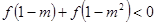 的实数
的实数 的取值集合;
的取值集合;
(3)当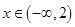 时,
时,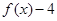 的值恒为负,求
的值恒为负,求 的取值范围.
的取值范围.
(本小题满分13分)国庆期间襄阳某体育用品专卖店抓住商机大量购进某特许商品进行销售,该特许产品的成本为20元/个,每日的销售量 (单位:个)与单价
(单位:个)与单价 (单位:元)之间满足关系式
(单位:元)之间满足关系式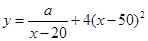 ,(其中
,(其中 ,
, 为常数).当销售价格为40元/个时,每日可售出该商品401个.
为常数).当销售价格为40元/个时,每日可售出该商品401个.
(1)求 的值及每日销售该特许产品所获取的总利润
的值及每日销售该特许产品所获取的总利润 ;
;
(2)试确定单价 的值,使所获得的总利润
的值,使所获得的总利润 最大.[来
最大.[来
(本小题满分12分)已知向量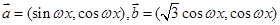 ,函数f(x)=2
,函数f(x)=2 的最小正周期为
的最小正周期为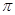 .(
.(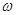 >0)
>0)
(1)求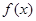 的递减区间;
的递减区间;
(2)在 中,
中, 分别是
分别是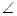 A、
A、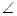 B、
B、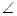 C的对边,若
C的对边,若 ,
, ,
, 的面积为
的面积为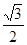 ,求
,求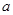 的值.
的值.
(本小题满分12分) 设函数 的定义域为集合
的定义域为集合 ,函数
,函数 的定义域为集合
的定义域为集合 .(1)求
.(1)求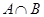 ;(2)若
;(2)若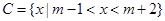 ,
, ,求实数
,求实数 的取值范围.
的取值范围.