如图,从 到
到 有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为
有6条网线,数字表示该网线单位时间内可以通过的最大信息量,现从中任取3条网线且使每条网线通过最大信息量,设这三条网线通过的最大信息之和为 .
.
(1)当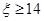 时,线路信息畅通,求线路信息畅通的概率;
时,线路信息畅通,求线路信息畅通的概率;
(2)求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分) (Ⅰ)小问7分,(Ⅱ)小问5分.)
已知O为坐标原点,向量=(sinα,1),=(cosα,0),=(-sinα,2),点P是直线AB上的一点,且点B分有向线段的比为1.
(1)记函数f(α)=·,α∈,讨论函数f(α)的单调性,并求其值域;
(2)若O、P、C三点共线,求|+|的值.
(本小题满分12分),(Ⅰ)小问5分,(Ⅱ)小问7分)
设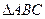 的内角A、B、C的对边长分别为a、b、c,且3
的内角A、B、C的对边长分别为a、b、c,且3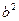 +3
+3 -3
-3 =4
=4 bc .
bc .
(Ⅰ) 求sinA的值;
(Ⅱ)求 的值.
的值.
(本小题满分12分), (Ⅰ)小问5分,(Ⅱ)小问7分.)
已知函数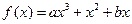 (其中常数a,b∈R),
(其中常数a,b∈R), 是奇函数.
是奇函数.
(Ⅰ)求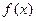 的表达式;
的表达式;
(Ⅱ)讨论 的单调性,并求
的单调性,并求 在区间上的最大值和最小值.
在区间上的最大值和最小值.
在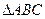 中,已知内角A、B、C所对的边分别为a、b、c,
中,已知内角A、B、C所对的边分别为a、b、c,
向量 ,
, 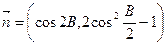 ,且
,且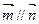
(I)求锐角B的大小;
(II)如果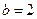 ,求
,求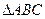 的面积
的面积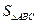 的最大值。
的最大值。
(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分. )
已知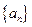 是首项为19,公差为-2的等差数列,
是首项为19,公差为-2的等差数列, 为
为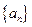 的前
的前 项和.
项和.
(Ⅰ)求通项 及
及 ;
;
(Ⅱ)设 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列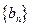 的通项公式及其前
的通项公式及其前 项和
项和 .
.