【2015高考新课标1,理23】选修4-4:坐标系与参数方程
在直角坐标系 中,直线
中,直线 :
:
 =
= 2,圆
2,圆 :
: ,以坐标原点为极点,
,以坐标原点为极点,  轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(Ⅰ)求 ,
, 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线 的极坐标方程为
的极坐标方程为 ,设
,设 与
与 的交点为
的交点为 ,
, ,求
,求 的面积.
的面积.
如图,在底角为 的等腰梯形
的等腰梯形 中,已知
中,已知 ,
, 分别为
分别为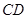 ,
,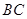 的中点.设
的中点.设 ,
, .
.
(1)试用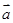 ,
,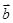 表示
表示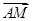 ,
, ;
;
(2)若 ,试求
,试求 的值.
的值.
已知函数 ,其中
,其中 为常数,
为常数, 为自然对数的底数.
为自然对数的底数.
(1)求 的单调区间;
的单调区间;
(2)若 ,且
,且 在区间
在区间 上的最大值为
上的最大值为 ,求
,求 的值;
的值;
(3)当 时,试证明:
时,试证明: .
.
某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 ,其中
,其中 ,
, 为常数,已知销售价格为4元/千克时,每日可销售出该商品5千克;销售价格为4.5元/千克时,每日可销售出该商品2.35千克.
为常数,已知销售价格为4元/千克时,每日可销售出该商品5千克;销售价格为4.5元/千克时,每日可销售出该商品2.35千克.
(1)求 的解析式;
的解析式;
(2)若该商品的成本为2元/千克,试确定销售价格 的值,使商场每日销售该商品所获得的利润
的值,使商场每日销售该商品所获得的利润 最大.
最大.
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组 ,第2组
,第2组 ,第3组
,第3组 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)上表是年龄的频率分布表,求正整数 的值;
的值;
(2)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组的人数分别是多少?
(3)在(2)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1人年龄在第3组的概率.
已知函数
 d的最大值为2,
d的最大值为2, 是集合
是集合 中的任意两个元素,且
中的任意两个元素,且 的最小值为
的最小值为 .
.
(1)求函数 的解析式及其对称轴;
的解析式及其对称轴;
(2)若 ,求
,求 的值.
的值.