已知直线 (
( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.
将曲线C的极坐标方程化为直角坐标方程;
设点 的直角坐标为
的直角坐标为 ,直线
,直线 与曲线C 的交点为
与曲线C 的交点为 ,
, ,求
,求 的值.
的值.
 的外接圆半径
的外接圆半径 ,角
,角 的对边分别是
的对边分别是 ,且
,且
(1)求角 和边长
和边长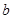 ;
;
(2)求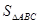 的最大值及取得最大值时的
的最大值及取得最大值时的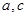 的值,并判断此时三角形的形状.
的值,并判断此时三角形的形状.
已知函数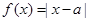 .
.
(1)若 的解集为
的解集为 ,求实数
,求实数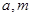 的值.
的值.
(2)当 且
且 时,解关于
时,解关于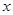 的不等式
的不等式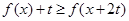 .
.
如图,已知⊙O的半径为1,MN是⊙O的直径,过M点作⊙O的切线AM,C是AM的中点,AN交⊙O于B点,若四边形BCON是平行四边形.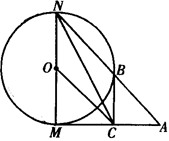
(Ⅰ)求AM的长;
(Ⅱ)求sin∠ANC.
已知函数f(x)=alnx+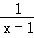 (a≠0)在(0,
(a≠0)在(0, )内有极值.
)内有极值.
(I)求实数a的取值范围;
(II)若x1∈(0, ),x2∈(2,+∞)且a∈[
),x2∈(2,+∞)且a∈[ ,2]时,求证:f(x1)﹣f(x2)≥ln2+
,2]时,求证:f(x1)﹣f(x2)≥ln2+ .
.
在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: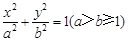 的离心率
的离心率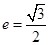 ,且椭圆C上一点
,且椭圆C上一点 到点Q
到点Q 的距离最大值为4,过点
的距离最大值为4,过点 的直线交椭圆
的直线交椭圆 于点
于点
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P为椭圆上一点,且满足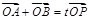 (O为坐标原点),当
(O为坐标原点),当 时,求实数
时,求实数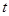 的取值范围.
的取值范围.