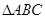 中,三个内角A、B、C所对的边分别为
中,三个内角A、B、C所对的边分别为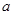 、
、 、
、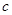 ,若
,若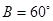 ,
,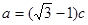 .
.
(Ⅰ)求角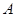 的大小;
的大小;
(Ⅱ)已知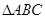 的面积为
的面积为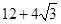 ,求函数
,求函数 的最大值.
的最大值.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,CE∥AB。
(Ⅰ)求证:CE⊥平面PAD;
(Ⅱ)若PA=AB=1,AD=3,且CD与平面PAD所成的角为45°,求二面角B—PE—A的正切值。
设函数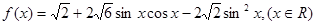
(I)对 的图像作如下变换:先将
的图像作如下变换:先将 的图像向右平移
的图像向右平移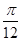 个单位,再将横坐标伸长到原来的2倍,纵坐标不变,得到函数
个单位,再将横坐标伸长到原来的2倍,纵坐标不变,得到函数 的图像,求
的图像,求 的解析式;
的解析式;
(II)已知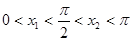 ,且
,且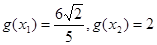 ,求
,求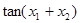 的值。
的值。
(本小题满分10分)选修4-5:不等式选讲
已知 ,且
,且 ,求证:
,求证: ≥8。
≥8。
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是 ,直线
,直线 的参数方程是
的参数方程是 。
。
(1)将曲线C的极坐标方程化为直角坐标方程;
(2)设直线 与
与 轴的交点是M,N是曲线C上一动点,求
轴的交点是M,N是曲线C上一动点,求 的最大值。
的最大值。
(本小题满分10分)选修4-1:几何证明选讲
如图,圆O的半径OB垂直于直径AC,M为OA上一点,BM的延长线交圆O于N,过N点的切线交CA的延长线于P。
(1)求证:PM2=PA·PC
(2)若圆O的半径为 ,OA=
,OA= OM,求MN的长。
OM,求MN的长。