已知数列{an}为等差数列,a3=5,a7=13,数列{bn}的前n项和为Sn,且有Sn=2bn-1,
(1)求{an},{bn}的通项公式.
(2)若cn=anbn,{cn}的前n项和为Tn,求Tn.
在平面直角坐标系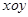 中,曲线
中,曲线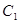 的参数方程为
的参数方程为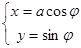 (
(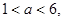
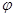 为参数),在以原点
为参数),在以原点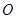 为极点,
为极点,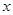 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线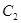 的极坐标方程为
的极坐标方程为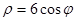 ,射线
,射线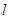 的方程为
的方程为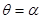 ,又
,又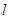 与
与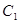 的交点为
的交点为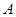 ,
,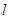 与
与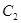 的除极点外的另一个交点为
的除极点外的另一个交点为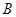 ,当
,当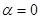 时,
时,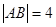 .
.
(1)求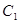 的普通方程,
的普通方程,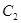 的直角坐标方程;
的直角坐标方程;
(2)设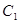 与
与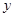 轴正半轴的交点为
轴正半轴的交点为 ,当
,当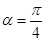 时,求直线
时,求直线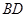 的参数方程.
的参数方程.
如图,四边形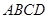 是☉
是☉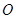 的内接四边形,
的内接四边形, 不经过点
不经过点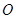 ,
,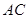 平分
平分 ,经过点
,经过点 的直线分别交
的直线分别交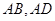 的延长线于点
的延长线于点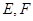 ,且
,且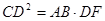 ,证明:
,证明: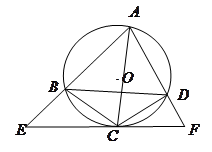
(1)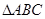 ∽
∽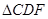 ;
;
(2)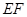 是☉
是☉ 的切线.
的切线.
已知函数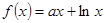 ,其中
,其中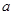 为常数,设
为常数,设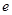 为自然对数的底数.
为自然对数的底数.
(1)当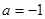 时,求
时,求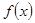 的最大值;
的最大值;
(2)若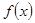 在区间
在区间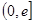 上的最大值为
上的最大值为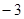 ,求
,求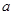 的值.
的值.
已知椭圆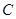 的对称中心为原点
的对称中心为原点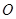 ,焦点在
,焦点在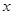 轴上,左、右焦点分别为
轴上,左、右焦点分别为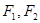 ,且
,且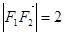 ,点
,点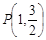 在该椭圆上.
在该椭圆上.
(1)求椭圆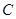 的方程;
的方程;
(2)过点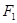 的直线
的直线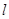 与椭圆
与椭圆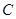 相交于
相交于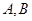 两点,若
两点,若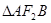 的面积为
的面积为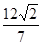 ,求以
,求以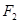 为圆心且与直线
为圆心且与直线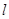 相切的圆的方程.
相切的圆的方程.
在三棱柱 中,侧面
中,侧面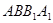 为矩形,
为矩形,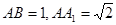 ,
,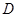 为
为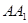 的中点,
的中点,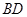 与
与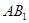 交于点
交于点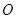 ,
,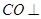 侧面
侧面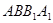 .
.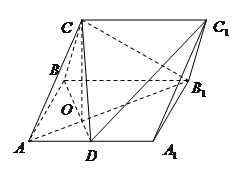
(1)证明: ;
;
(2)若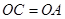 ,求三棱柱
,求三棱柱 的体积.
的体积.