已知椭圆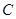 的对称中心为原点
的对称中心为原点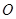 ,焦点在
,焦点在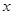 轴上,左、右焦点分别为
轴上,左、右焦点分别为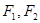 ,且
,且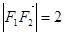 ,点
,点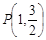 在该椭圆上.
在该椭圆上.
(1)求椭圆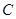 的方程;
的方程;
(2)过点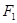 的直线
的直线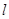 与椭圆
与椭圆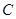 相交于
相交于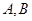 两点,若
两点,若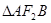 的面积为
的面积为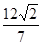 ,求以
,求以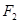 为圆心且与直线
为圆心且与直线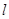 相切的圆的方程.
相切的圆的方程.
设 在R上是偶函数.
在R上是偶函数.
(1)求 的值;
的值;
(2)证明 在
在 上是增函数.(12分)
上是增函数.(12分)
已知函数 .
.
(1)求 的最小正周期;
的最小正周期;
(2)当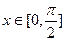 时,求
时,求 的最小值及取得最小值时
的最小值及取得最小值时 的集合.(12分)
的集合.(12分)
已知函数 , 且
, 且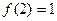 .
.
(1)求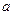 的值; (
的值; ( 2)求
2)求 的值;(3)解不等式
的值;(3)解不等式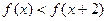 .(10分
.(10分 )
)
(本小题满分14分)
已知数列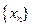 的前n项和为
的前n项和为 满足
满足 ,
,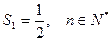
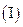 猜想数列
猜想数列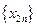 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(Ⅱ) 对于数列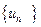 若存在常数M>0,对任意的
若存在常数M>0,对任意的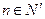 ,恒有
,恒有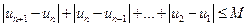 ,,则称数列
,,则称数列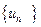 为B-数列。问数列
为B-数列。问数列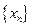 是B-数列吗?并证明你的结论。
是B-数列吗?并证明你的结论。
(本题满分14分)
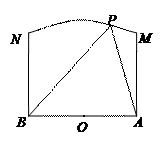
如图,两个工厂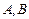 相距
相距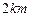 ,点
,点 为
为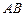 的中点,现要在以
的中点,现要在以 为圆心,
为圆心,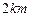 为半
为半 径的圆弧
径的圆弧 上的某一点
上的某一点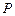 处建一幢办公楼,其中
处建一幢办公楼,其中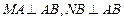 .据测算此办公楼受工厂
.据测算此办公楼受工厂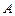 的“噪音影响度”与距离
的“噪音影响度”与距离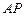 的平方成反比,比例系数是1,办公楼受工厂
的平方成反比,比例系数是1,办公楼受工厂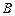 的“噪音影响度” 与距离
的“噪音影响度” 与距离
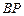 的平方也成反比,比例系数是4,办公楼受
的平方也成反比,比例系数是4,办公楼受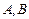 两厂的“总噪音影响度”
两厂的“总噪音影响度”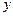 是受
是受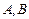 两厂“噪音影响度”的和,设
两厂“噪音影响度”的和,设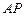 为
为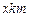 .
.
(Ⅰ)求“总噪音影响度” 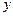 关于
关于 的函数关系,
的函数关系,
并求出该函数的定义域;
(Ⅱ)当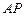 为多少时,“总噪音影响度”最小?
为多少时,“总噪音影响度”最小?