（本小题满分15分）
某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元，该厂为鼓励销售商订购，决定当一次订购量超过100个时，每多订购一个，订购的全部零件的出厂单价就降低0.02元，但实际出厂单价不能低于51元.
（Ⅰ）当一次订购量为多少个时，零件的实际出厂单价恰降为51元？
（Ⅱ）设一次订购量为x个，零件的实际出厂单价为P元，写出函数P=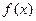
的表达式；
（Ⅲ）当销售商一次订购500个零件时，该厂获得的利润是多少元？如果订购1000个，利润又是多少元？（工厂售出一个零件的利润=实际出厂单价－成本）
（本小题满分12分）
写出命题“一组对边平行且相等的四边形是平行四边形”的逆命题，否命题，逆否命题，并且判断其真假.
两直线分别过A(-a,0),B(a,0)且绕A,B旋转，它们在y轴上的截距分别为b1，b2，b1，b2=a2，求两直线交点的轨迹方程．
已知函数
，试研究该函数的性质．
已知函数
在
上为增函数,且
,
为常数,
.
(1)求的值;
(2)若
在
上为单调函数,求
的取值范围;
(3)设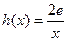
,若在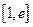
上至少存在一个
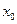，使得
成立，求的取值范围.
已知椭圆C的中心在原点，焦点在
轴上,椭圆上的点到左、右焦点
的距离之和为
，离心率
.
（1）求椭圆C的方程；
（2）过左焦点
的直线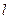
与椭圆C交于点
,以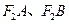
为邻边作平行四边形
,求该平行四边形对角线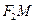
的长度的取值范围.