(本小题满分10分)某校高一年级开设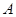 ,
, ,
, ,
,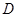 ,
,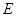 五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选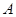 课程,不选
课程,不选 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(Ⅰ)求甲同学选中 课程且乙同学未选中
课程且乙同学未选中 课程的概率;
课程的概率;
(Ⅱ)用 表示甲、乙、丙选中
表示甲、乙、丙选中 课程的人数之和,求
课程的人数之和,求 的分布列和数学期望.
的分布列和数学期望.
设 是由满足下列条件的函数
是由满足下列条件的函数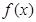 构成的集合:“①函数
构成的集合:“①函数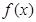 的导数
的导数 满足
满足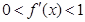 ;②方程
;②方程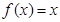 有实数根”.
有实数根”.
(I)判断函数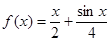 是否是集合
是否是集合 中的元素,并说明理由;
中的元素,并说明理由;
(II)集合 中的元素
中的元素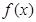 具有下面的性质:若
具有下面的性质:若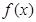 的定义域为D,则对于任意
的定义域为D,则对于任意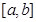
 D,都存在
D,都存在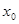

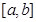 ,使得等式
,使得等式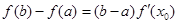 成立”,试用这一性质证明:方程
成立”,试用这一性质证明:方程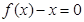 只有一个实数根;
只有一个实数根;
(III)设 是方程
是方程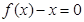 的实数根,求证:对于
的实数根,求证:对于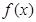 定义域中任意的
定义域中任意的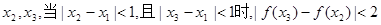 .
.
已知函数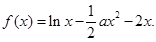
(I)若 ,求
,求 的增区间;
的增区间;
(II)若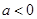 ,且函数
,且函数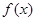 存在单调递减区间,求
存在单调递减区间,求 的取值范围;
的取值范围;
(III)若 且关于
且关于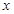 的方程
的方程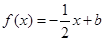 在
在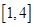 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数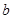 的取值范围.
的取值范围.
数列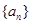 满足
满足 其中
其中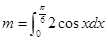 .
.
(I)求 ,猜想
,猜想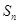 ;(II)请用数学归纳法证明之.
;(II)请用数学归纳法证明之.
高考数学考试中共有10道选择题,每道选择题都有4个选项,其中有且仅有一个是正确的.评分标准规定:“在每小题给出的四个选项中,只有一项是符合题目要求的,答对得5分,不答或答错得0分”.某考生每道选择题都选出了一个答案,能确定其中有6道题的答案是正确的,而其余题中,有两道题都可判断出有两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只能乱猜.
试求出该考生的选择题:
(I)得30分的概率;
(II)得多少分的概率最大;
(III)所得分数 的数学期望.
的数学期望.
已知在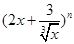 的展开式中,第
的展开式中,第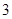 项的二项式系数与第2项的二项式系数的比为
项的二项式系数与第2项的二项式系数的比为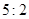 .
.
(I)求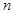 的值;
的值;
(II)求含 的项的系数;
的项的系数;
(III)求展开式中系数最大的项.