已知某市的光明中学、市图书馆和光明电影院在同一直线上，它们之间的距离如图所示．小张星期天上午带了75元现金先从光明中学乘出租车去了市图书馆，付费9元；中午再从市图书馆乘出租车去了光明电影院，付费12.6元．若该市出租车的收费标准是：不超过3公里计费为m元，3公里后按n元/公里计费．
（1）求m，n的值，并直接写出车费y（元）与路程x（公里）（x＞3）之间的函数关系式；
（2）如果小张这天外出的消费还包括：中午吃饭花费15元，在光明电影院看电影花费25元．问小张剩下的现金够不够乘出租车从光明电影院返回光明中学？为什么？
先化简，再求值 
，其中 
= 
．
(8分)2010年湛江市某校为了了解400名学生体育加试成绩，从中抽取了部分学生的成绩(满分为40分，而且成绩均为整数)，绘制了频数分布表与频数分布直方图(如图)，请结合图表信息解答下列问题：
(1)补全频数分布表与频数分布直方图；
(2)如果成绩在31分以上(含31分)的同学属于优良请你估计全校约有多少人达到优良水平；
(3)加试结束后，校长说：“2008年，初一测试时，优良人数只有90人，经过两年的努力，才有今天的成绩……．”假设每年优良人数增长速度一样，请你求出每年的平均增长率(结果精确到1%)．
(8分)如图，在□ABCD中，点E、F是对角线BD上的两点，且BE＝DF．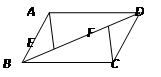
求证：(1)△ABE≌△CDF；(2)AE∥CF．
(8分)端午节吃粽子时中华民族的传统习惯．五月初五早晨，小丽的妈妈用不透明装着一些粽子（粽子除内部馅料不同外，其他一切相同），其中香肠馅粽子两个，还有一些绿豆馅粽子，现小丽从中任意拿出一个是香肠馅粽子的概率为．
(1)求袋子中绿豆馅粽子的个数；
(2)小丽第一次任意拿出一个粽子(不放回)，第二次再拿出一个粽子，请你用树形图或列表法，求小丽两次拿到的都是绿豆馅粽子的概率．
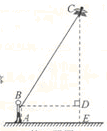
(8分)如图，小明在公园放风筝，拿风筝线的手B离地面高度AB为1.5m，风筝飞到C处时的线长BC为30m，这时测得∠CBD＝60º．求此时风筝离地面的高度（精确到0.1m，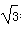
≈1.73）．