已知数列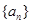 的前n项和是
的前n项和是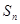 ,且
,且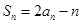
(1)证明: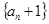 为等比数列;
为等比数列;
(2)证明: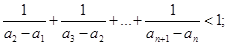
(3)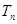 为数列
为数列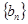 的前n项和,设
的前n项和,设 ,是否存在正整数m,k,使
,是否存在正整数m,k,使 成立,若存在,求出m,k;若不存在,说明理由.
成立,若存在,求出m,k;若不存在,说明理由.
在平面直角坐标系xOy中,动点P到直线l:x=2的距离是到点F(1,0)的距离的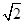 倍.
倍.
(1)求动点P的轨迹方程;
(2)设直线FP与(1)中曲线交于点Q,与l交于点A,分别过点P和Q作l的垂线,垂足为M,N,问:是否存在点P使得△APM的面积是△AQN面积的9倍?若存在,求出点P的坐标;若不存在,说明理由.
已知椭圆C1: =1,椭圆C2以C1的短轴为长轴,且与C1有相同的离心率.
=1,椭圆C2以C1的短轴为长轴,且与C1有相同的离心率.
(1)求椭圆C2的方程;
(2)设直线l与椭圆C2相交于不同的两点A、B,已知A点的坐标为(-2,0),点Q(0,y0)在线段AB的垂直平分线上,且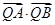 =4,求直线l的方程.
=4,求直线l的方程.
在数列{an}中,a1=1,{an}的前n项和Sn满足2Sn=an+1.
(1)求数列{an}的通项公式;
(2)若存在n∈N*,使得λ≤ ,求实数λ的最大值.
,求实数λ的最大值.
已知{an}为等差数列,且a2=-1,a5=8.
(1)求数列{|an|}的前n项和;
(2)求数列{2n·an}的前n项和.
已知数列{an}的前n项和Sn满足Sn+an+ n-1=2(n∈N*),设cn=2nan.
n-1=2(n∈N*),设cn=2nan.
(1)求证:数列{cn}是等差数列,并求数列{an}的通项公式.
(2)按以下规律构造数列{bn},具体方法如下:
b1=c1,b2=c2+c3,b3=c4+c5+c6+c7,…,第n项bn由相应的{cn}中2n-1项的和组成,求数列{bn}的通项bn.