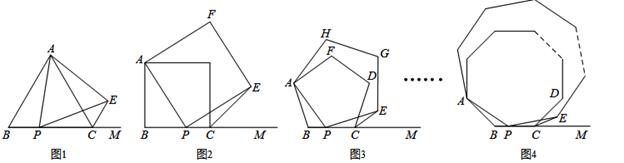
在图1、图2、图3、图4中,点P在线段BC上移动(不与B、C重合),M在BC的延长线上.
(1)如图1,△ABC和△APE均为正三角形,连接CE.
①求证:△ABP≌△ACE.
②∠ECM的度数为 °.
(2)①如图2,若四边形ABCD和四边形APEF均为正方形,连接CE .则∠ECM的度数为 °.
②如图3,若五边形ABCDF和五边形APEGH均为正五边形,连接CE.则∠ECM的度数为 °.
(3)如图4,n边形ABC…和n边形APE…均为正n边形,连接CE,请你探索并猜想∠ECM的度数与正多边形边数n的数量关系(用含n的式子表示∠ECM的度数),并利用图4(放大后的局部图形)证明你的结论.