某通讯公司推出①、②两种通讯收费方式供用户选择，其中一种有月租费，另一种无月租费，且两种收费方式的通讯时间x（分钟）与收费y（元）之间的函数关系如图所示．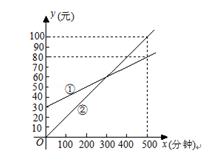
（1）有月租费的收费方式是 （填①或②），月租费是 元；
（2）分别求出①、②两种收费方式中y与自变量x之间的函数关系式；
（3）请你根据用户通讯时间的多少，给出经济实惠的选择建议．
如图，在ΔABC和ΔDCB中，AC与BD相交于点， AB = DC，AC = BD.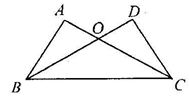
(1)求证: ΔABC≌ΔDCB；
(2) Δ0BC的形状是。(直接写出结论，不需证明) 。
把下列各数分别填入相应的集合中：
-
， 
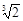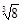， 0.232323 
有理数集合无理数集合
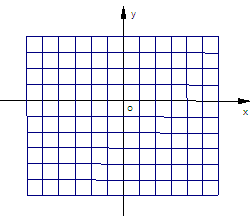
已知点A（a，0）、B（b，0），且
．
（1）求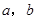
的值；
（2）在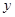
轴上是否存在点C，使得△ABC的面积是12？若存在，求出点C的坐标；若不存在，请说明理由；
（3）点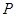
是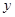轴正半轴上一点，且到
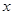轴的距离为3，若点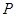沿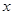轴负半轴方向以每秒1个长度单位平行移动至Q，当运动的时间
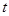为多少秒时，四边形ABPQ的面积S为15个平方单位？写出此时Q点的坐标．
如图，△ABC中，∠A=90º，∠ABC与∠ACB的角平分线交于点I，△ABC的外角∠DBC与∠BCE的角平分线交于P.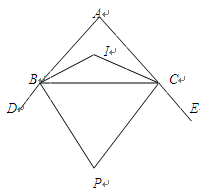
（1）则∠BIC= ，∠P= （直接写出答案）；
（2）若∠A的度数为xº时，求∠BIC，∠P的度数.
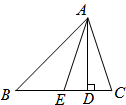
如图，△ABC中，∠B=
，∠C=
，AE是△ABC的角平分线，AD是BC上的高.求∠EAD的度数.