如图,在平面直角坐标系xOy中,函数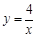 (x>0)的图象与一次函数y=kx-k的图象交点为A(m,2).
(x>0)的图象与一次函数y=kx-k的图象交点为A(m,2).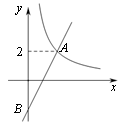
(1)求一次函数的表达式;
(2)设一次函数y=kx-k的图象与y轴交于点B,如果P是x轴上一点,且满足△PAB的面积是4,请直接写出P的坐标.
如图,直线 与 轴、 轴分别交于 , 两点,抛物线 与直线 分别交 轴的正半轴于点 和第一象限的点 ,连接 ,得 为坐标原点).若抛物线与 轴正半轴交点为点 ,设 是点 , 间抛物线上的一点(包括端点),其横坐标为 .
(1)直接写出点 的坐标和抛物线的解析式;
(2)当 为何值时, 面积 取得最小值和最大值?请说明理由;
(3)求满足 的点 的坐标.

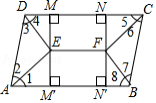
如图,在 中, ,四个角的平分线 , , , 的交点分别是 , ,过点 , 分别作 与 间的垂线 与 ,在 与 上的垂足分别是 , 与 , ,连接 .
(1)求证:四边形 是矩形;
(2)已知: , , ,求 的长.
山地自行车越来越受中学生的喜爱.一网店经营的一个型号山地自行车,今年一月份销售额为30000元,二月份每辆车售价比一月份每辆车售价降价100元,若销售的数量与上一月销售的数量相同,则销售额是27000元.
(1)求二月份每辆车售价是多少元?
(2)为了促销,三月份每辆车售价比二月份每辆车售价降低了 销售,网店仍可获利 ,求每辆山地自行车的进价是多少元?
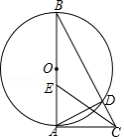
如图,在 中,以 为直径作 交 于点 , .
(1)求证: 是 的切线;
(2)点 是 上一点,若 , , 的半径是4,求 的长.
今年5月13日是“母亲节”,某校开展“感恩母亲,做点家务”活动为了了解同学们在母亲节这一天做家务情况,学校随机抽查了部分同学,并用得到的数据制成如下不完整的统计表:
|
做家务时间(小时) |
人数 |
所占百分比 |
|
组:0.5 |
15 |
|
|
组:1 |
30 |
|
|
组:1.5 |
|
|
|
组:2 |
3 |
|
|
合计 |
|
|
(1)统计表中的 , ;
(2)小君计算被抽查同学做家务时间的平均数是这样的:
第一步:计算平均数的公式是 ,
第二步:该问题中 , , , , ,
第三步: (小时)
小君计算的过程正确吗?如果不正确,请你计算出正确的做家务时间的平均数;
(3)现从 , 两组中任选2人,求这2人都在 组中的概率(用树形图法或列表法).