如图,在平面直角坐标系中,点A、C分别在x轴、y轴上,四边形ABCO为矩形,AB=16,点D与点A关于y轴对称,tan∠ACB=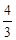 ,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.
,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.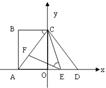
(1)求AC的长和点D的坐标;
(2)说明△AEF与△DCE相似;
(3)当△EFC为等腰三角形时,求点E的坐标.
题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.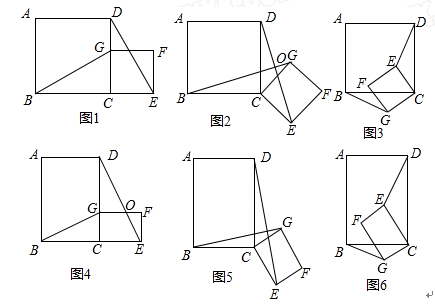
问题探究:(1)①如图1所示,当G在CD边上时,猜想线段BG、DE的数量关系及所在直线的位置关系.(不要求证明)
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,请选择图2或图3证明你的判断.
类比研究:(2)若将原题中的“正方形”改为“矩形”(如图所示),且
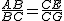 =k(其中k>0),请写出线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断(仅证数量关系).
=k(其中k>0),请写出线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断(仅证数量关系).
拓展应用:(3)在(1)中图2中,连接DG、BE,若AB=3,EF=2,求BE2+DG2的值.
小王从A地前往B地,到达后立刻返回,他与A地的距离y(千米)和所用的时间x(小时)之间的函数关系如图所示。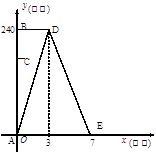
(1)小王从B地返回A地用了多少小时?
(2)求小王出发6小时后距A地多远?
(3)在A、B之间有一C地,小王从去时途经C地,到返回时路过C地,共用了2小时20分,求A、C两地相距多远?
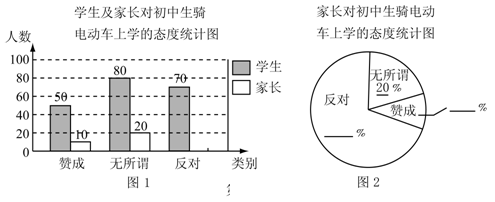
“初中生骑电动车上学”的现象越来越受到社会的关注,某校利用假期,随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法,统计整理制作了如下的统计图,请回答下列问题:(1)这次抽查的家长总人数为
(2)请补全条形统计图和扇形统计图;
(3)求这次接受调查的学生中,随机抽查一个学生恰好抽到持“无所谓”态度的概率.
如图, 为⊙
为⊙ 的直径,
的直径, 为⊙
为⊙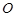 的切线,
的切线,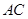 交⊙
交⊙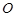 于点
于点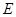 ,
,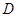 为
为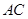 上一点,
上一点, .
.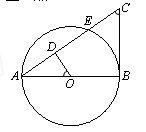
(1)求证:
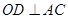 ;
;(2)若
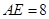 ,
,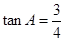 ,求
,求 的长
的长
热气球的探测器显示,从热气球看一栋高楼顶部的仰角为 ,看这栋高楼底部的俯角为
,看这栋高楼底部的俯角为 ,热气球与高楼的水平距离为66 m,这栋高楼有多高?(结果精确到0.1 m,参考数据:
,热气球与高楼的水平距离为66 m,这栋高楼有多高?(结果精确到0.1 m,参考数据: )
)