(本小题满分12分)
设数列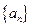 的前
的前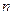 项和为
项和为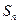 .已知
.已知 ,
,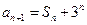 ,
, .
.
(Ⅰ)设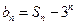 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)若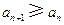 ,
, ,求
,求 的取值范围.。
的取值范围.。
(本小题满分1 2分)
2分)
已知函数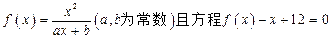 有两个实根为
有两个实根为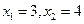 。
。
(1)求函数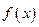 的解析式;
的解析式;
(2)解关 于
于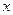 的不等式
的不等式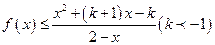
(本小题满分1 0分)
0分)
已知函数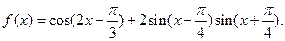
(1)求函数 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;
(2)求函数 在区间
在区间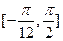 上的值域。
上的值域。
(本小题满分14分)已知函数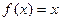 ,函数
,函数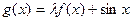 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数.
(I)求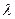 的最大值;
的最大值;
(II)若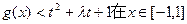 上恒成立,求t的取值范围;
上恒成立,求t的取值范围;
(Ⅲ)讨论关于x的方程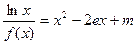 的根的个数.
的根的个数.
S△ABC=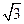 ,求a的值.
,求a的值.
(本小题满分13分)已知椭圆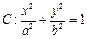
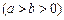 的离心率为
的离心率为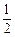 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线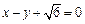 相切.
相切.
(Ⅰ)求椭圆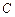 的方程;
的方程;
(Ⅱ)设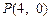 ,
,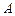 ,
,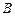 是椭圆
是椭圆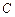 上关于
上关于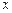 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结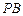 交椭圆
交椭圆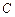 于另一点
于另一点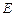 ,证明直线
,证明直线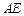 与
与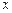 轴相交于定点
轴相交于定点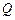 .
.
S△ABC=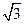 ,求a的值.
,求a的值.