设函数f(x)=(x+1)ln(x+1),若对所有的x≥0,都有f(x)≥ax成立,求实数a的取值范围.
数列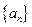 满足
满足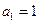 ,
,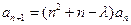 (
(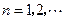 ),
),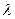 是常数.(Ⅰ)当
是常数.(Ⅰ)当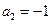 时,求
时,求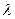 及
及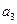 的值;(Ⅱ)数列
的值;(Ⅱ)数列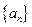 是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;(Ⅲ)求
是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;(Ⅲ)求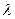 的取值范围,使得存在正整数
的取值范围,使得存在正整数 ,当
,当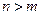 时总有
时总有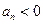 .
.
已知二次函数y=f(x)的图像经过坐标原点,其导函数为f¢(x)=6x-2,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图像上.(Ⅰ)求数列{an}的通项公式;(Ⅱ)设bn=,Tn是数列{bn}的前n项和,求使得Tn<对所有n∈N*都成立的最小正整数m;
设数列{an}的首项a1∈(0,1),an=,n=2,3,4,….(Ⅰ)求{an}的通项公式;(Ⅱ)设bn=an,证明bn<bn+1,其中n为正整数.
已知函数f(x)=logax+2x和g(x)=2loga(2x+t-2)+2x(a>0,a≠1,t∈R)的图象在x=2处的切线互相平行.(Ⅰ)求t的值;(Ⅱ)设F(x)=g(x)-f(x),当x∈[1,4]时,F(x)≥2恒成立,求a的取值范围.