一个盒子里装有标号为1,2,3,…,n的n(n>3,且n∈N*)张标签,现随机地从盒子里无放回地抽取两张标签,记X为这两张标签上的数字之和,若X=3的概率为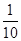 .
.
(1)求n的值;
(2)求X的分布列.
如图,在△ABC中,已知B=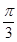 ,AC=4
,AC=4 ,D为BC边上一点.
,D为BC边上一点.
(I)若AD=2,S△ABC=2 ,求DC的长;
,求DC的长;
(Ⅱ)若AB=AD,试求△ADC的周长的最大值.
(本小题满分14分)
已知函数f(x)= x
x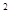 -ax + (a-1)
-ax + (a-1)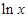 ,
,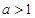 .
.
(I)讨论函数 的单调性;
的单调性;
(II)若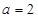 ,数列
,数列 满足
满足 .
.
若首项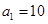 ,证明数列
,证明数列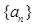 为递增数列;
为递增数列;
若首项为正整数,数列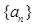 递增,求首项的最小值.
递增,求首项的最小值.
(本小题满分12分)
有甲、乙两种相互独立的预防措施可以降低某地区某灾情的发生.单独采用甲、乙预防措施后,灾情发生的概率分别为0.08和0.10,且各需要费用60万元和50万元.在不采取任何预防措施的情况下发生灾情的概率为0.3.如果灾情发生,将会造成800万元的损失.(设总费用=采取预防措施的费用+可能发生灾情损失费用)
(I)若预防方案允许甲、乙两种预防措施单独采用,他们各自总费用是多少?
(II)若预防方案允许甲、乙两种预防措施单独采用、联合采用或不采用,请确定预防方案使总费用最少的那个方案.
(本小题满分12分)设点P的坐标为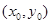 ,直线l的方程为
,直线l的方程为 .请写出点P到直线l的距离,并加以证明.
.请写出点P到直线l的距离,并加以证明.
(本小题满分12分)
如图,FD垂直于矩形ABCD所在平面,CE//DF,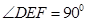 .
.
(Ⅰ)求证:BE//平面ADF;
(Ⅱ)若矩形ABCD的一个边AB =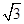 ,EF =
,EF =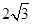 ,则另一边BC的长为何值时,二面角B-EF-D的大小为450?
,则另一边BC的长为何值时,二面角B-EF-D的大小为450?