(本小题满分14分)
已知函数f(x)= x
x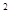 -ax + (a-1)
-ax + (a-1)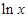 ,
,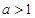 .
.
(I)讨论函数 的单调性;
的单调性;
(II)若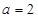 ,数列
,数列 满足
满足 .
.
若首项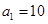 ,证明数列
,证明数列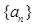 为递增数列;
为递增数列;
若首项为正整数,数列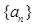 递增,求首项的最小值.
递增,求首项的最小值.
(本小题12分)设函数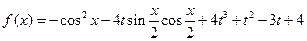 ,
,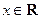 ,其中
,其中 ,将
,将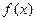 的最小值记为
的最小值记为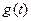 .
.
(I)求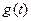 的表达式;
的表达式;
(II)设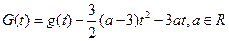 ,讨论
,讨论 在区间
在区间 内的单调性.
内的单调性.
(本小题12分)如图,一只船在海上由西向东航行,在 处测得某岛
处测得某岛 的方位角为北偏东
的方位角为北偏东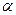 角,前进
角,前进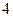
 后在
后在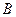 处测得该岛的方位角为北偏东
处测得该岛的方位角为北偏东 角,已知该岛周围
角,已知该岛周围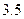
 范围内有暗礁,现该船继续东行.
范围内有暗礁,现该船继续东行.
(I)若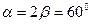 ,问该船有无触礁危险?如果没有,请说明理由;如果有,那么该船自
,问该船有无触礁危险?如果没有,请说明理由;如果有,那么该船自 处向东航行多少距离会有触礁危险?
处向东航行多少距离会有触礁危险?
(II)当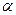 与
与 满足什么条件时,该船没有触礁危险?
满足什么条件时,该船没有触礁危险?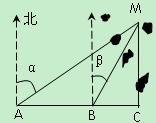
(本小题12分)已知函数 .
.
(I)若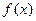 在
在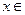 [1,+∞
[1,+∞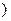 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(II)若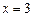 是
是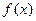 的极值点,求
的极值点,求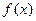 在
在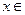 [1,a]上的最小值和最大值.
[1,a]上的最小值和最大值.
(本小题12分)设函数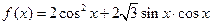 ,
,
(I)求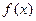 的最小正周期以及单调增区间;
的最小正周期以及单调增区间;
(II)当 时,求
时,求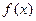 的值域;
的值域;
(Ⅲ)若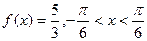 ,求
,求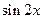 的值.
的值.
(本小题10分)在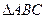 中,
中,  分别是
分别是 的对边,
的对边,
已知 是方程
是方程 的两个根,且
的两个根,且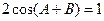 .
.
求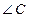 的度数和
的度数和 的长度.
的长度.