(1) 在直角坐标系xOy中,曲线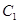 的参数方程为
的参数方程为 为参数),M为
为参数),M为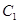 上的动点,P点满足
上的动点,P点满足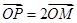 ,点P的轨迹为曲线
,点P的轨迹为曲线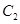 .已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线
.已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线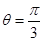 与
与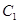 的异于极点的交点为A,与
的异于极点的交点为A,与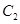 的异于极点的交点为B,求|AB|.
的异于极点的交点为B,求|AB|.
(2) 某旅游景点给游人准备了这样一个游戏,他制作了“迷尼游戏板”:在一块倾斜放置的矩形胶合板上钉着一个形如“等腰三角形”的八行铁钉,钉子之间留有空隙作为通道,自上而下第1行2个铁钉之间有1个空隙,第2行3个铁钉之间有2个空隙,…,第8行9个铁钉之间有8个空隙(如图所示).东方庄家的游戏规则是:游人在迷尼板上方口放人一球,每玩一次(放入一球就算玩一次)先付给庄家2元.若小球到达①②③④号球槽,分别奖4元、2元、0元、-2元.(一个玻璃球的滚动方式:通过第1行的空隙向下滚动,小球碰到第二行居中的铁钉后以相等的概率滚入第2行的左空隙或右空隙.以后小球按类似方式继续往下滚动,落入第8行的某一个空隙后,最后掉入迷尼板下方的相应球槽内).恰逢周末,某同学看了一个小时,留心数了数,有80人次玩.试用你学过的知识分析,这一小时内游戏庄家是赢是赔? 通过计算,你得到什么启示?
(本题12分)已知函数 ,当
,当 时,
时, ;当
;当 时,
时,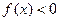 .(1)
.(1)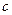 为何值时
为何值时 的解集为
的解集为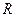 ;(2)求
;(2)求 在
在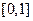 内的值域.
内的值域.
(本题12分)对于函数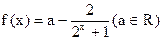 为奇函数(Ⅰ)求
为奇函数(Ⅰ)求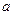 的值;(Ⅱ)用函数单调性定义及指数函数性质证明:
的值;(Ⅱ)用函数单调性定义及指数函数性质证明:  在
在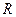 上是增函数。
上是增函数。
(本题12分)某一中校办工厂生产学生校服的固定成本为20000元,每多生产一件需要增加投入100元,已知总收益R(x)满足函数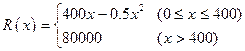 ,其中x是校服的月产量,问:(1)将利润表示为关于月产量x的函数
,其中x是校服的月产量,问:(1)将利润表示为关于月产量x的函数 .(2)当月产量为何值时,工厂所获利润最大?最大利润为多少元?(总收益=总成本+利润)
.(2)当月产量为何值时,工厂所获利润最大?最大利润为多少元?(总收益=总成本+利润)
(本题12分)已知定义在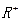 上的函数
上的函数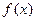 满足下列条件:1对定义域内任意
满足下列条件:1对定义域内任意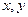 ,恒有
,恒有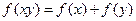 ;2当
;2当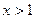 时
时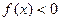 ;3
;3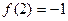 (1)求
(1)求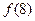 的值;
的值;
(2)求证:函数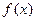 在
在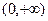 上为减函数;(3)解不等式 :
上为减函数;(3)解不等式 :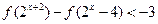
(本题14分)设函数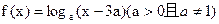 , 当P(x,y)是函数y=f(x)图像上的点时,点
, 当P(x,y)是函数y=f(x)图像上的点时,点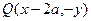 是函数y=g(x)图象上的点。①写出函数y=g(x)的解析式;②若当
是函数y=g(x)图象上的点。①写出函数y=g(x)的解析式;②若当 时,恒有
时,恒有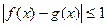 试确定a的取值范围。
试确定a的取值范围。