某校举办安全法规知识竞赛，从参赛的高一、高二学生中各抽出100人的成绩作为样本．对高一年级的100名学生的成绩进行统计，得到成绩分布的频率分布直方图如图：
（1）若规定60分以上（包括60分）为合格，计算高一年级这次知识竞赛的合格率；
（2）将上述调查所得到的频率视为概率.现在从该校大量高一学生中，采用随机抽样方法每次抽取1名学生，抽取3次，记被抽取的3名学生中的合格人数为
.若每次抽取的结果是相互独立的，求的分布列和期望
；
| |
高一 |
高二 |
合计 |
| 合格人数 |
|
|
|
| 不合格人数 |
|
|
|
| 合计 |
|
|
|
（3）若高二年级这次知识竞赛的合格率为60%，由以上统计数据填写2×2列联表，并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系” ．
已知函数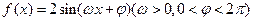
在一个周期内的图象如图所示。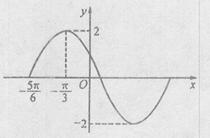
（1）求
的值
；
（2）在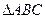
中，设内角A、B、C所对边的长分别为a、b、c。
若
，求b的值。
如图，在三棱锥P－ABC中，PA⊥底面ABC，PA＝AB，∠ABC＝60°，∠BCA＝90°，点D、E分别在棱PB、PC上，且DE∥BC.
(1)求证：BC⊥平面PAC；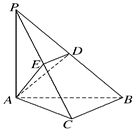
(2)当D为PB的中点时，求AD与平面PAC所成的角的正弦值；
(3)是否存在点E使得二面角A－DE－P为直二面角？并说明理由．
(8分).
一个多面体的直观图和三视图如图所示，其中M、N分别是AB、AC的中点，G是DF上的一动点.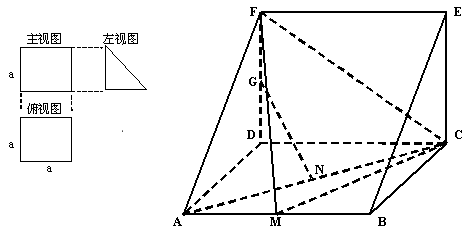
( 1) 求该多面体的体积.
（2）求证：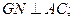
（3）当FG=GD时，在棱AD上确定一点P，使得GP//平面FM
C,并给出证明.
如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营救．甲船立即前往救援，同时把消息告知在甲船的南偏西30
，相距10海里C处的乙船，试问乙船应朝北偏东多少度的方向沿直线前往B处救援？（可能用到的数据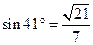
，
）
．如图，在四面体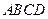
中， 
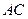平行于截面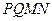
(1)若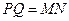
,证明
∥平面；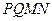
（2）若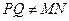
，猜想三条直线
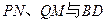位置关系，并证明之.