如图,在平面直角坐标系 中,
中,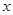 轴在地平面上,
轴在地平面上,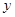 轴垂直于地面,
轴垂直于地面,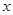 轴、
轴、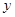 轴上的单位长度都为
轴上的单位长度都为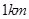 ,某炮位于坐标原点处,炮弹发射后,其路径为抛物线
,某炮位于坐标原点处,炮弹发射后,其路径为抛物线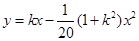 的一部分,其中
的一部分,其中 与炮弹的发射角有关且
与炮弹的发射角有关且 .
.
(1)当 时,求炮弹的射程;
时,求炮弹的射程;
(2)对任意正数 ,求炮弹能击中的飞行物的高度
,求炮弹能击中的飞行物的高度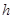 的取值范围;
的取值范围;
(3)设一飞行物(忽略大小)的高度为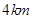 ,试求它的横坐标
,试求它的横坐标 不超过多少
不超过多少 时,炮弹可以击中它.(答案精确到
时,炮弹可以击中它.(答案精确到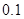 ,
, 取
取 )
)
在数列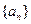 中,
中,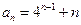 ,
,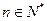 .
.
(1)求数列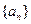 的前
的前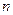 项和
项和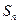 ;(2)证明不等式
;(2)证明不等式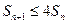 ,对任意
,对任意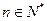 皆成立。
皆成立。
已知等差数列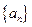 的前项和为
的前项和为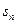 ,
,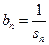 ,且
,且 ,
,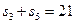 .
.
⑴.求数列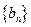 的通项公式;⑵.求证:
的通项公式;⑵.求证: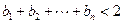 .
.
如果一个数列的各项都是实数,且从第二项开始,每一项与它前一项的平方差是相同的常数,则称该数列为等方差数列,这个常数叫这个数列的公方差.
(1)设数列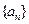 是公方差为
是公方差为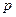 (p>0,an >0)的等方差数列,
(p>0,an >0)的等方差数列,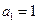 求
求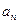 的通项公式;
的通项公式;
(2)若数列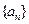 既是等方差数列,又是等差数列,证明该数列为常数列
既是等方差数列,又是等差数列,证明该数列为常数列
已知f(x+1)=x2-4,等差数列{an}中,a1=f(x-1), a2=- ,a3=f(x).
,a3=f(x).
(1)求x值;
(2)求a2+a5+a8+…+a26的值.
下表给出一个“等差数阵”:
| 4 |
7 |
() |
() |
() |
…… |
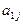 |
…… |
| 7 |
12 |
() |
() |
() |
…… |
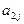 |
…… |
| () |
() |
() |
() |
() |
…… |
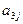 |
…… |
| () |
() |
() |
() |
() |
…… |
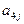 |
…… |
| …… |
…… |
…… |
…… |
…… |
…… |
…… |
…… |
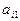 |
 |
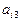 |
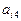 |
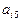 |
…… |
 |
…… |
| …… |
…… |
…… |
…… |
…… |
…… |
…… |
…… |
其中每行、每列都是等差数列, 表示位于第i行第j列的数。
表示位于第i行第j列的数。
(I)写出 的值;(II)写出
的值;(II)写出 的计算公式;
的计算公式;