(本小题满分12分)已知集合A=[-2,2],B=[-1,1],设M={(x,y)|x∈A,y∈B},在集合M内随机取出一个元素(x,y).
(1)求以(x,y)为坐标的点落在圆x2+y2=1内的概率;
(2)求以(x,y)为坐标的点到直线x+y=0的距离不大于 的概率.
的概率.
已知函数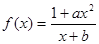
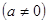 是奇函数,并且函数
是奇函数,并且函数 的图像经过点(1,3),(1)求实数
的图像经过点(1,3),(1)求实数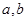 的值;(2)求函数
的值;(2)求函数 的值域.
的值域.
已知向量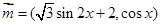 ,
,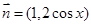 ,设函数
,设函数 ,
, .
.
(1)求 的最小正周期与最大值;
的最小正周期与最大值;
(2)在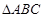 中,
中, 分别是角
分别是角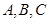 的对边,若
的对边,若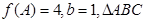 的面积为
的面积为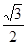 ,求
,求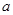 的值.
的值.
已知函数 ,
,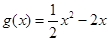 .
.
(Ⅰ)设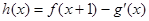 (其中
(其中 是
是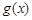 的导函数),求
的导函数),求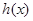 的最大值;
的最大值;
(Ⅱ)求证:当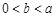 时,有
时,有 ;
;
(Ⅲ)设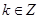 ,当
,当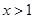 时,不等式
时,不等式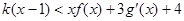 恒成立,求
恒成立,求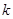 的最大值.
的最大值.
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为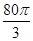 立方米,且
立方米,且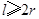 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为 千元,设该容器的建造费用为
千元,设该容器的建造费用为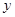 千元.
千元.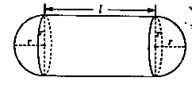
(Ⅰ)写出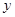 关于
关于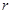 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(Ⅱ)求该容器的建造费用最小时的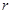 .
.
已知函数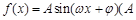 >0,
>0,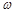 >0,
>0,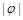 <
<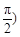 的图像与
的图像与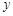 轴的交点为(0,1),它在
轴的交点为(0,1),它在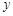 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为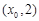 和
和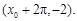
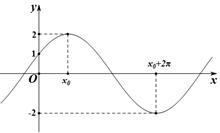
(1)求 的解析式及
的解析式及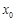 的值;
的值;
(2)若锐角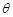 满足
满足 ,求
,求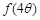 的值.
的值.