(本小题满分12分)已知一个袋子中有3个白球和3个红球,这些球除颜色外完全相同.
(Ⅰ)每次从袋中取出一个球,取出后不放回,直到取到一个红球为止,求取球次数 的分布列和数学期望
的分布列和数学期望 ;
;
(Ⅱ)每次从袋中取出一个球,取出后放回接着再取一个球,这样取3次,求取出红球次数 的数学期望
的数学期望 .
.
(本小题共13分)
已知某个几何体的三视图如图(主视图的弧线是半圆),根据图中标出的数据,
(Ⅰ)求这个组合体的表面积;
(Ⅱ)若组合体的底部几何体记为 ,其中
,其中 为正方形.
为正方形.
(i)求证: ;
;
(ii)设点 为棱
为棱 上
上 一点,求直线
一点,求直线 与平面
与平面 所成角的正弦值的取值范围.
所成角的正弦值的取值范围.

(本小题共13分)
如图,当甲船位于 处时获悉,在其正东方向相距20海里的
处时获悉,在其正东方向相距20海里的 处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西
处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西 30
30 ,相距10海里
,相距10海里 处的乙船.
处的乙船.
(Ⅰ)求处于 处的乙船和遇险渔船间的距离;
处的乙船和遇险渔船间的距离; (Ⅱ)设乙船沿直线
(Ⅱ)设乙船沿直线 方向前往
方向前往 处救援,其方向与
处救援,其方向与 成
成 角,求
角,求
 的值域.
的值域.
已知二次函数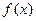 的二次项系数为
的二次项系数为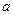 ,且不等式
,且不等式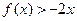 的解集为
的解集为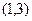 。
。
(Ⅰ)若方程 有两个相等的根,求
有两个相等的根,求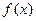 的解析式;
的解析式;
(Ⅱ)若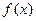 的最大值为正数,求
的最大值为正数,求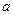 的取值范围。
的取值范围。
设数列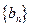 的前
的前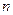 项和为
项和为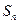 ,且
,且 ,数列
,数列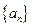 为等差数列,公差大于0,且
为等差数列,公差大于0,且 是方程
是方程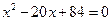 的两个实根
的两个实根
(1) 求数列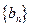 、
、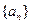 的通项公式;(2) 若
的通项公式;(2) 若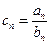 ,求数列
,求数列 的前
的前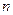 项和
项和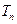
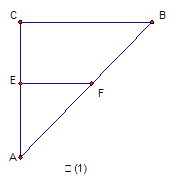
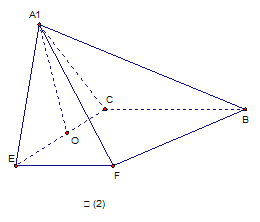
如图(1),△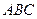 是等腰直角三角形,
是等腰直角三角形,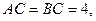 E、F分别为AC、AB的中点,将△AEF沿EF折起,使
E、F分别为AC、AB的中点,将△AEF沿EF折起,使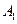 在平面BCEF上的射影O恰好为EC的中点,得到图(2)。
在平面BCEF上的射影O恰好为EC的中点,得到图(2)。
(Ⅰ)求证: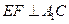 ;(Ⅱ)求三棱锥
;(Ⅱ)求三棱锥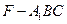 的体积。
的体积。