(本小题共13分)
如图,当甲船位于 处时获悉,在其正东方向相距20海里的
处时获悉,在其正东方向相距20海里的 处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西
处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西 30
30 ,相距10海里
,相距10海里 处的乙船.
处的乙船.
(Ⅰ)求处于 处的乙船和遇险渔船间的距离;
处的乙船和遇险渔船间的距离; (Ⅱ)设乙船沿直线
(Ⅱ)设乙船沿直线 方向前往
方向前往 处救援,其方向与
处救援,其方向与 成
成 角,求
角,求
 的值域.
的值域.
.如图所示,已知A、B两点的距离为100海里,B在A的北偏东30°处,甲船自A以50海里/小时的速度向B航行,同时乙船自B以30海里/小时的速度沿方位角150°方向航行.问航行几小时两船之间的距离最短?
如果有穷数列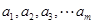 (
(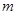 为正整数)满足条件
为正整数)满足条件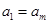 ,
,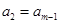 ,…,
,…,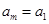 ,即
,即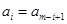 (
(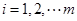 ),我们称其为“对称数列”.例如,数列1,2,5,2,1与数列8,4,2,2,4,8都是“对称数列”.
),我们称其为“对称数列”.例如,数列1,2,5,2,1与数列8,4,2,2,4,8都是“对称数列”.
(1)设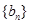 是7项的“对称数列”,其中
是7项的“对称数列”,其中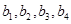 是等差数列,且
是等差数列,且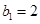 ,
,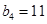 .依次写出
.依次写出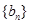 的每一项;
的每一项;
(2)设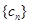 是49项的“对称数列”,其中
是49项的“对称数列”,其中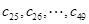 是首项为1,公比为2的等比数列,求
是首项为1,公比为2的等比数列,求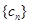 各项的和S.
各项的和S.
在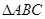 中,已知
中,已知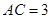 ,
,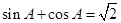 ,
,
(1)求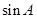 的值;
的值;
(2)若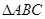 的面积
的面积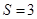 ,求BC的值.
,求BC的值.
(本小题满分14分)设函数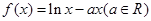 (e=2.718 28……是自然对数的底数).
(e=2.718 28……是自然对数的底数).
(1)判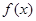 断的单调性;
断的单调性;
(2)当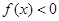 在(0,+∞)上恒成立时,求a的取值范围;
在(0,+∞)上恒成立时,求a的取值范围;
(3)证明:当 (0,+∞)时,
(0,+∞)时,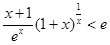 .
.
(本小题满分13分)有两个投资项目 ,根据市场调查与预测,A项目的利润与投资成正比,其关系如图甲,B项目的利润与投资的算术平方根成正比,其关系如图乙.(注:利润与投资单位:万元)
,根据市场调查与预测,A项目的利润与投资成正比,其关系如图甲,B项目的利润与投资的算术平方根成正比,其关系如图乙.(注:利润与投资单位:万元)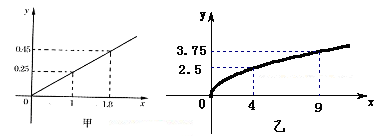
(1)分别将 两个投资项目的利润表示为投资
两个投资项目的利润表示为投资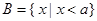 (万元)的函数关系式;
(万元)的函数关系式;
(2)现将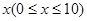 万元投资
万元投资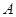 项目,
项目,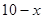 万元投资
万元投资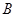 项目.
项目.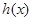 表示投资A项目所得利润与投资
表示投资A项目所得利润与投资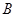 项目所得利润之和.求
项目所得利润之和.求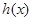 的最大值,并指出
的最大值,并指出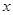 为何值时,
为何值时,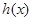 取得最大值
取得最大值