(本小题满分14分)设函数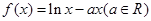 (e=2.718 28……是自然对数的底数).
(e=2.718 28……是自然对数的底数).
(1)判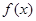 断的单调性;
断的单调性;
(2)当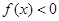 在(0,+∞)上恒成立时,求a的取值范围;
在(0,+∞)上恒成立时,求a的取值范围;
(3)证明:当 (0,+∞)时,
(0,+∞)时,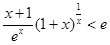 .
.
如图所示,长方体ABCD-A1B1C1D1中,AB=a,BC=b,BB1=c,并且a>b>c>0.
求沿着长方体的表面自A到C1的最短线路的长.
如图所示的几何体中,四边形AA1B1B是边长为3的正方形,CC1=2,CC1∥AA1,这个几何体是棱柱吗?若是,指出是几棱柱.若不是棱柱,请你试用一个平面截去一部分,使剩余部分是一个棱长为2的三棱柱,并指出截去的几何体的特征,在立体图中画出截面.
圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积等于392 cm2,母线与轴的夹角是45°,求这个圆台的高、母线长和两底面半径.
正四棱台AC1的高是17 cm,两底面的边长分别是4 cm和16 cm,求这个棱台的侧棱长和斜高.
棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,
求图中三角形(正四面体的截面)的面积.