(本小题满分13分)已知函数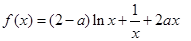 .
.
(Ⅰ)当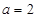 时,求函数
时,求函数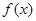 的极值;
的极值;
(Ⅱ)
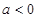 时,讨论
时,讨论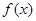 的单调性;
的单调性;
(Ⅲ)若对任意的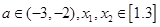 恒有
恒有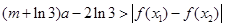 成立,求实数
成立,求实数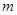 的取值范围.
的取值范围.
(本小题满分12分)抛物线 的焦点为F,
的焦点为F,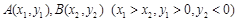 在抛物线上,且存在实数
在抛物线上,且存在实数 ,使
,使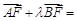
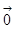 ,
,
(Ⅰ)求直线AB的方程;
(Ⅱ)求△AOB的外接圆的方程。
(本小题满分13分)在平面直角坐标系 中,已知椭圆
中,已知椭圆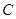 :
: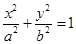 (
( )的左焦点为
)的左焦点为 ,且点
,且点 在
在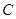 上.
上.
(Ⅰ)求椭圆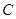 的方程;
的方程;
(Ⅱ)已知直线 的斜率为2且经过椭圆
的斜率为2且经过椭圆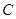 的左焦点.求直线
的左焦点.求直线 与该椭圆
与该椭圆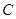 相交的弦长。
相交的弦长。
(本小题满分13分)已知集合A=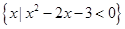 ,B=
,B=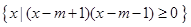 ,
,
(Ⅰ)当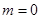 时,求
时,求 .
.
(Ⅱ)若 :
: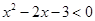 ,
, :
: ,且
,且 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数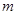 的取值范围。
的取值范围。
(本小题满分13分)实数 满足圆的标准方程
满足圆的标准方程 ,
,
(Ⅰ)求 的最小值;
的最小值;
(Ⅱ)求定点 到圆上点的最大值.
到圆上点的最大值.
设函数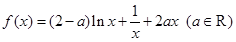 .
.
(1)当 时,求
时,求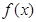 的极值;
的极值;
(2)当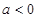 时,求
时,求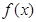 的单调区间;
的单调区间;
(3)若对任意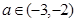 及
及 ,恒有
,恒有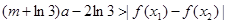 成立,求
成立,求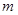 的取值范围
的取值范围